

Advanced level vector algebra

- By koushiadmin
- (0) comments
- June 29, 2025
Advanced level vector algebra
For serious JEE Advanced aspirants, mastering advanced vector calculus concepts such as Gradient, Divergence, and Curl is crucial. These vector operators form the backbone of many topics in physics and engineering, including electromagnetism, fluid dynamics, and vector fields.
Vector triple product:
1. ![]()
![]() (
(![]()
![]()
![]() ) = (
) = (![]() .
.![]() )
)![]() – (
– (![]() .
.![]() )
)![]()
2. (![]() ×
×![]() ) ×
) × ![]() = –
= – ![]() ×(
×(![]() ×
×![]() ) = – [(
) = – [(![]() .
.![]() )
)![]() – (
– (![]() .
.![]() )
)![]() ] = (
] = (![]() .
.![]() )
)![]() – (
– (![]() .
.![]() )
)![]()
3. (![]() ×
×![]() ).(
).(![]() ×
×![]() )×(
)×(![]() ×
×![]() ) = (
) = (![]() .
.![]() ×
×![]() )²
)²
Prove: Let, ![]() ×
×![]() =
= ![]() so, (
so, (![]() ×
×![]() )×(
)×(![]() ×
×![]() ) =
) = ![]() ×(
×(![]() ×
×![]() ) = (
) = (![]() .
.![]() )
)![]() – (
– (![]() .
.![]() )
)![]()
= (![]() ×
×![]() .
.![]() )
)![]() – (
– (![]() ×
×![]() .
.![]() )
)![]()
= (![]() .
.![]() ×
×![]() )
)![]() – (
– (![]() .
.![]() ×
×![]() )
)![]()
= ( ![]() .
.![]() ×
×![]() )
)![]() – 0 [as
– 0 [as ![]() ×
×![]() = 0]
= 0]
![]() (
(![]() ×
×![]() ).(
).(![]() ×
×![]() )×(
)×(![]() ×
×![]() ) = (
) = (![]() ×
×![]() ).(
).(![]() .
.![]() ×
×![]() )
)![]() = (
= (![]() .
.![]() ×
×![]()
![]()
Reciprocal sets of vectors: Let us consider, ![]() ,
, ![]() and
and ![]() are three sets of vectors with their reciprocal sets of vectors
are three sets of vectors with their reciprocal sets of vectors ![]() ,
, ![]() and
and ![]() respectively then,
respectively then, ![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]() 0
0

 and
and 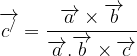
[the volume of the body is v = ![]() ]
]
![]()

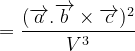
![]()
Differential Geometry:
Let us consider, C is the space curve is defined by the function ![]() . The vector in the direction of tangent to C is
. The vector in the direction of tangent to C is ![]() .
.
If s is the arc length measured from a fixed point on C represents the scalar value of u, then ![]() =
= ![]() is unit tangent vector to C.
is unit tangent vector to C.

If ![]() changes with respect to s, then
changes with respect to s, then ![]() represents the value of curvature of C. The direction of
represents the value of curvature of C. The direction of ![]() is the normal at that point on curve C. So,
is the normal at that point on curve C. So, ![]() =
= ![]() where
where ![]() is the unit normal vector to the curve and K = curvature .The radius of curvature is
is the unit normal vector to the curve and K = curvature .The radius of curvature is ![]() =
= ![]() .
.
A unit vector ![]() perpendicular to the plane of
perpendicular to the plane of ![]() and
and ![]() is
is ![]() =
= ![]() ×
×![]() is called binormal to the curve.
is called binormal to the curve. ![]() ,
, ![]() and
and ![]() represent trihedral or triad ordinate system at any point of curve C.
represent trihedral or triad ordinate system at any point of curve C.
Example: A space curve is represented by x = 4Cost, y = 4Sint and z = 3t. Calculate (i) unit tangent vector and (ii) unit normal vector.
The position vector for any point on the curve is ![]() = 4cost
= 4cost![]() + 4sin t
+ 4sin t![]() + 3t
+ 3t![]()
![]() = – 4sint
= – 4sint![]() + 4cost
+ 4cost![]() + 3
+ 3![]()
![]() =
= ![]() =
= ![]() =
= ![]() = 5
= 5
The unit tangent vector ![]() =
= ![]() =
= ![]() .
.![]() = –
= – ![]() sint
sint![]() +
+ ![]() cost
cost![]() +
+ ![]()
![]()
![]() = –
= – ![]() cost
cost![]() –
– ![]() sin t
sin t![]()
![]() =
= ![]() = –
= – ![]() cost
cost![]() –
– ![]() sin t
sin t![]()
![]() =
= ![]()
![]() = K.1
= K.1
[where ![]() is the unit normal vector of the curve]
is the unit normal vector of the curve]
The curvature is K = + ![]()
![]()
![]() =
= ![]()
![]() = – cost
= – cost![]() – sin t
– sin t![]() .
.
Normal and tangent vector at any point on the surface:
Let us consider, a surface is represented by the equation ![]() =
=![]() (u, v) . A curve can be represented for a fixed value of u = u0as
(u, v) . A curve can be represented for a fixed value of u = u0as ![]() =
=![]() (u0, v . Similarly for u = u1, the curve is represented
(u0, v . Similarly for u = u1, the curve is represented ![]() =
=![]()
![]() . Therefore,
. Therefore, ![]() =
=![]() (u, v) represents a curve which moves in space and generates a surface s.
(u, v) represents a curve which moves in space and generates a surface s.
![]() (Keeping v = v0 constant) represents a tangent vector at point P to the curve v = v0 at point P. similarly,
(Keeping v = v0 constant) represents a tangent vector at point P to the curve v = v0 at point P. similarly,![]() (Keeping u = u0 constant) at point P represents a tangent vector to the curve u = u0 at point P.
(Keeping u = u0 constant) at point P represents a tangent vector to the curve u = u0 at point P.
So, ![]() ×
× ![]() is the vector normal to the surface at P.
is the vector normal to the surface at P.
Example: The equation of a surface is represented by z = x2 + y2. Find the equation for the tangent plane at pointP (2, -1, 2).
Let us consider, x = u, y = v and z = u2 + v2 where (x, y, z) represents a point P on the surface. The position vector of a point P (x, y, z)on the surface is represented by ![]() = u
= u![]() + v
+ v![]() + (u² + v²)
+ (u² + v²)![]() .
.

Example: The equation of a surface is represented by z = x2+ y2. Find the equation for the tangent plane at pointP (2,-1,2).
Let us consider, x =u, y = v and z = u2+ v2where (x,y,z) represents a point P on the surface. The position vector of a point P (x,y,z)on the surface is represented by ![]()
![]() u
u![]() +v
+v![]() +(u²+v²)
+(u²+v²)![]() .
.
Therefore, ![]() + 2u
+ 2u![]() =4
=4![]() (where u = 2)and
(where u = 2)and ![]() =
=![]() +2v
+2v![]() =
= ![]() -2
-2![]() (where v = -1)
(where v = -1)
The normal vector to the surface at point P is ![]() =
=![]() ×
× ![]() =(
=(![]() +4
+4![]() )×(
)×(![]() -2
-2![]() ) = -4
) = -4![]() + 2
+ 2![]() +
+ ![]() .
.
![]() =
= ![]() ×
× ![]() =
= 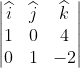 = -4
= -4![]() +2
+2![]() +
+![]()
The position vector of point P(2, -1, 2) is ![]() = 2
= 2![]() –
–![]() +2
+2![]() . Let us consider, another point Q(x,y,z) is on a plane which is the tangent plane at point P (2, -1, 2).
. Let us consider, another point Q(x,y,z) is on a plane which is the tangent plane at point P (2, -1, 2).
The position vector of point Q on the tangent plane is ![]() = x
= x![]() + y
+ y![]() +z
+z![]() . The vector
. The vector![]() = (
= (![]() –
–![]() ) = [(x
) = [(x![]() +y
+y![]() +z
+z![]() ) – (2
) – (2![]() –
– ![]() + 2
+ 2![]() )] = (x – 2)
)] = (x – 2) ![]() + (y+1)
+ (y+1) ![]() + (z-2)
+ (z-2) ![]() represents a vector on the tangent plane. As
represents a vector on the tangent plane. As ![]() is the normal to the surface at point P(2, -1, 2), then
is the normal to the surface at point P(2, -1, 2), then ![]() is also perpendicular to
is also perpendicular to ![]() . Therefore,
. Therefore, ![]() .
.![]() = 0.
= 0.
So, [(x-2) ![]() + (y+1)
+ (y+1) ![]() +(z-2)
+(z-2) ![]() ].(-4
].(-4![]() +2
+2![]() +
+![]() ) = 0
) = 0
Or, -4(x-2) + 2(y+1) + (z-2) = 0
Or, -4x +8 + 2y + 2 + z – 2 = 0
![]() -4x + 2y + z = – 8
-4x + 2y + z = – 8
This represents the equation of the tangent plane at point P on the surface.
Vector differential operator: This is called as del and written as ∇.∇ is also called as nabla.
Where ∇ = ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() . This vector operator possesses the properties analogous to that of vector.
. This vector operator possesses the properties analogous to that of vector.
The gradient: ∇![]() = (
= ( ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() )
) ![]() =
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ( where
( where ![]() is the differentiable scaler field.
is the differentiable scaler field.
The component of ∇![]() , in the direction of
, in the direction of ![]() is ∇
is ∇![]() .
. ![]() is called the directional derivative of
is called the directional derivative of ![]() in the direction of
in the direction of ![]() .
.
The divergence: Let us consider, ![]() =
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() is the differentiable vector field. The divergence of
is the differentiable vector field. The divergence of ![]() is ∇.
is ∇.![]() =(
=( ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ). = (
). = ( ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() ) =
) = ![]() +
+ ![]() +
+ ![]() .
.
The curl: Let us consider, ![]() =
= ![]()
![]() +
+ ![]()
![]() is the differentiable vector field. Then the curl or rotation of
is the differentiable vector field. Then the curl or rotation of ![]() is ∇×
is ∇×![]() . Here, ∇×
. Here, ∇×![]() =
=  =
= ![]() (
( ![]() –
– ![]() ) + (
) + ( ![]() –
– ![]() ) + (
) + ( ![]() –
– ![]() ).
).
Prove that ∇![]() is a vector perpendicular to the surface
is a vector perpendicular to the surface ![]() (x, y, z) = c where c is a constant.
(x, y, z) = c where c is a constant.
Let us consider, ![]() =x
=x![]() +y
+y![]() + z
+ z![]() be the position vector to any point P (x, y, z) on the surface. Then,
be the position vector to any point P (x, y, z) on the surface. Then, ![]() =dx
=dx![]() + dy
+ dy![]() + dz
+ dz ![]() lies in the tangent plane to the surface at point P.
lies in the tangent plane to the surface at point P.
But d![]() =
= ![]() dx +
dx + ![]() dy +
dy + ![]() dz = 0 [as
dz = 0 [as ![]() (x, y, z) = constant then, d
(x, y, z) = constant then, d![]() = 0]
= 0]
Or, ( ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() )
)
Or, ∇![]() .
.![]() = 0
= 0
Hence, ∇![]() is perpendicular to dr or to the surface.
is perpendicular to dr or to the surface.
Example: 1.Find unit normal vector to the surface x2y + 2xz = 4 at point (1, 1, 2)
The normal vector to the surface x2y + 2xz = 4 is ∇![]() = ∇( x2y + 2xz) = (2xy+2z)
= ∇( x2y + 2xz) = (2xy+2z) ![]() +
+ ![]()
![]() + 2x
+ 2x![]() +6
+6![]() +
+ ![]() + 2
+ 2![]() at (1, 1, 2)
at (1, 1, 2)
Unit normal to the surface = ![]() =
= ![]()
![]() +
+ ![]()
![]() +
+![]()
![]()
Another unit normal is – ![]()
![]() –
– ![]()
![]() –
–![]()
![]() opposite direction of the above vector.
opposite direction of the above vector.
Angular speed: A rigid body rotates about an axis through a point O with angular speed ![]() . The linear velocity of a point P of the body with position vector
. The linear velocity of a point P of the body with position vector ![]() is
is ![]() =
= ![]() ×
×![]() . [direction of is that in which a right-hand screw would advance under the given rotation].
. [direction of is that in which a right-hand screw would advance under the given rotation].
The point P rotates in a circle of radius r sin ![]() . The magnitude of linear velocity is v =
. The magnitude of linear velocity is v = ![]() r sin
r sin ![]()
∴![]() =
= ![]() ×
× ![]()
Conservative vector field: If , ∇ × ![]() = 0 then
= 0 then ![]() is conservative vector field.
is conservative vector field.
If ![]() = ∇
= ∇ ![]() then
then ![]() is known as scalar potential.
is known as scalar potential.
Example: 1. Prove ![]() = (2xy +
= (2xy + ![]() )
) ![]() +
+ ![]()
![]() + 3x
+ 3x![]()
![]() is conservative.
is conservative.
= =[ – ] + [ – ] + [ – ] = [0 – 0] + [3z2 – 3z2] + [2x – 2x] = 0
∇ × ![]() =
= 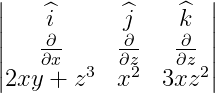 =
= ![]() [
[![]() ] +
] + ![]() [
[![]() –
– ![]() ] +
] + ![]() [
[ ![]() ] =
] = ![]() [0-0] +
[0-0] + ![]() [
[![]() ] +
] + ![]() [2x-2x] = 0
[2x-2x] = 0
- Find work done to move a particle from (2, -1, 1) to (1, 1,2) in this field. As W =

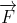 .
.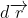 =
=  [(2xy +
[(2xy +  )
) =
= 
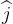 + 3x
+ 3x
 ].[dx
].[dx + dy
+ dy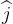 + dz
+ dz ]
]
W = ![]() (2xy +
(2xy +![]() )dx +
)dx + ![]() dy +3x
dy +3x![]() dz =
dz = ![]() d(
d(![]() y +
y + ![]() x) =
x) = ![]() = [1×1 + 8 ×1] – [4(-1) + 1×2] = 9 + 2 = 11
= [1×1 + 8 ×1] – [4(-1) + 1×2] = 9 + 2 = 11
Find scaler potential in previous problem.
3) Find scaler potential in previous problem.
![]() = ∇
= ∇ ![]() =
=![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() = (2xy +
= (2xy + ![]() )
)![]() +
+![]()
![]() + 3x
+ 3x![]()
![]()
Then, ![]() = 2xy +
= 2xy + ![]() so,
so, ![]() = ∫( 2xy +
= ∫( 2xy + ![]() )dx =
)dx = ![]() y +
y + ![]() x + f (y, z)
x + f (y, z)
And ![]() =
= ![]() so,
so, ![]() = ∫
= ∫ ![]() dy =
dy = ![]() y + g(x, z)
y + g(x, z)
And ![]() = 3x
= 3x![]() so,
so, ![]() = ∫3x
= ∫3x![]() dz = x
dz = x![]() + h(x, y)
+ h(x, y)
As ![]() is a particular function of x, y, z so f(y,z) = 0, g(x, z) =
is a particular function of x, y, z so f(y,z) = 0, g(x, z) = ![]() x and h(x, y) =
x and h(x, y) = ![]() y
y
∴ ![]() =
= ![]() y +
y + ![]() x
x
= Work ![]() =
= ![]() (1,1,2) –
(1,1,2) – ![]() (2, -1, 1)
(2, -1, 1)
- Find the work done in moving a particle in the force field given by
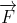 = 3zy
= 3zy  – 5z
– 5z 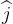 + 10x
+ 10x  along the curve x = t2+ 1, y = 2t2and z = t3 from t = 1 to t = 2.
along the curve x = t2+ 1, y = 2t2and z = t3 from t = 1 to t = 2.
The work done W = ∫dw = ∫![]() .
.![]() = ∫( 3xy
= ∫( 3xy ![]() – 5z
– 5z ![]() + 10x
+ 10x ![]() ). ( dx
). ( dx![]() + dy
+ dy ![]() + dz
+ dz ![]() )
)
= ∫ 3xydx – 5zdy + 10xdz)
= ![]() [3(
[3(![]() +1). 2
+1). 2![]() d(
d( ![]() +1 ) – 5
+1 ) – 5![]() d(2
d(2![]() ) + 10 (
) + 10 (![]() +1)d (
+1)d (![]() )
)
= ![]() [3(
[3(![]() +1). 2
+1). 2![]() .2tdt – 5
.2tdt – 5![]() . 4tdt + 10(
. 4tdt + 10(![]() +1) . 3
+1) . 3![]() dt]
dt]
= ![]() [12
[12![]() dt +12
dt +12![]() dt – 20
dt – 20![]() dt +30
dt +30![]() dt]
dt]
= ![]() ( 12
( 12![]() + 10
+ 10![]() + 12
+ 12![]() + 30
+ 30![]() )dt
)dt
= [2![]() + 2
+ 2![]() + 3
+ 3![]() + 10
+ 10![]() ]
]
= [2(![]() -1) + 2(
-1) + 2(![]() -1) + 3(
-1) + 3(![]() -1) + 10(
-1) + 10(![]() -1)
-1)
= 126 + 62 + 45 + 70 = 303.
- Calculate the work done to move a particle through a curve y = 2x2 from (0, 0) to (1, 2) in xy plane by the force
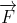 = 3xy
= 3xy –
–
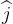 .
.
The work done is W= ![]()
![]() .
.![]() where
where ![]() = dx
= dx ![]() +dy
+dy![]() [z = 0 here]
[z = 0 here]
W =![]() dw =
dw = ![]() (3xy
(3xy![]() –
– ![]()
![]() ). (dx
). (dx![]() + dy
+ dy![]() )
)
= ![]() 3x (2
3x (2![]() )dx –
)dx –![]() d (2
d (2![]() )
)
= ![]() 6
6![]() dx –
dx – ![]() . 4xdx
. 4xdx
= ![]() 6
6![]() dx – 16
dx – 16![]() dx
dx
= – ![]()
- If
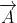 and
and  are two vectors, then findthe component of
are two vectors, then findthe component of 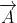 perpendicular to
perpendicular to  .
.
Let us consider, the vector perpendicular to![]() and
and![]() is
is ![]() ×
×![]() = AB sin
= AB sin ![]()
![]() where
where ![]() is unit vector perpendicular to the plane containing
is unit vector perpendicular to the plane containing ![]() and
and ![]() i.e. – Z axis here. So,
i.e. – Z axis here. So,
![]() = –
= – ![]()
∴ ![]() ×(
×(![]() ×
×![]() ) = -AB sin
) = -AB sin ![]() B
B![]() ×
×![]() = A
= A![]() sin
sin ![]()
![]()
∴ Asin ![]()
![]() = ×
= ×
where Asin ![]()
![]() is the component of
is the component of ![]() perpendicular to
perpendicular to ![]() .
.
Gauss’s divergence theorem:
![]()
![]()
![]() .
.![]() ds =
ds = ![]()
![]()
![]() (div
(div![]() ) dv
) dv
Volume integral of divergence of a vector ![]() in a vector field through a volume is equal to the surface integral of the normal component of
in a vector field through a volume is equal to the surface integral of the normal component of ![]() over the surface which enclose the volume.
over the surface which enclose the volume.
Stoke’s law:
![]()
![]() . d
. d![]() =
= ![]()
![]() curt
curt![]() .
.![]()
Line integral of the tangential comp. of a vector ![]() round any closed path is equal to the normal surface integral of the vector curl
round any closed path is equal to the normal surface integral of the vector curl![]() over the surface having the path as its boundary.
over the surface having the path as its boundary.
A force is defined as ![]() =
= ![]() . Calculate the work done along a semi-circular path with the origin as centre connecting the points (-1, 0) and (1, 0).
. Calculate the work done along a semi-circular path with the origin as centre connecting the points (-1, 0) and (1, 0).
(ii) along a straight line joining (-1, 0), (0, 1) and (0, 1), (1, 0). Comparing the two values, comment on the nature of the force.
Here ![]() .
.![]() =
= ![]()
Let us consider a = a cos ![]() and y = a sin
and y = a sin![]() . So, dx = – a sin
. So, dx = – a sin![]() d
d![]() and dy = a cos
and dy = a cos ![]() d
d![]()
Therefore, work done W ![]()
![]() .
.![]() =
= ![]()
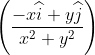 .(dx
.(dx![]() + dy
+ dy ![]() ) =
) = ![]()
![]() =
= ![]()
![]() =
=
![]() sin 2
sin 2![]() d
d![]() = 0
= 0
(ii) (a) Along a straight line joining (-1, 0) (0, 1): The equation of the straight line joining (-1, 0), (0, 1) is x + 1 = y or, dx = dy
Therefore, work done W = ![]()
![]() .
.![]() =
= ![]()
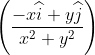 . (dx
. (dx![]() + dy
+ dy ![]() ) =
) = ![]()
![]() =
= ![]()
![]()
= ![]()
![]()
∴ ![]()
![]() .
.![]() =
= ![]()
![]()
![]() =
= ![]() . 2 [
. 2 [![]()
![]()
![]() =
= ![]()
(b) Along the straight line joining (0, 1), (1, 0):The equation of the straight line is given by y = 1 – x or, dy = – dx
Therefore, work done W = ![]()
![]() .
.![]() =
=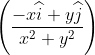 . (dx
. (dx![]() + dy
+ dy ![]() ) =
) = ![]()
![]() =
= ![]()
![]() =
=![]()
![]()
∴ ![]()
![]() .
.![]() = –
= – ![]()
![]()
![]() = –
= – ![]() .2
.2![]() = –
= – ![]()
∴ ![]()
![]() .
.![]() joining the two points (-1, 0) and (1, 0) via the above straight lines =
joining the two points (-1, 0) and (1, 0) via the above straight lines = ![]() –
– ![]() = 0
= 0
The force ![]() is conservative.
is conservative.

