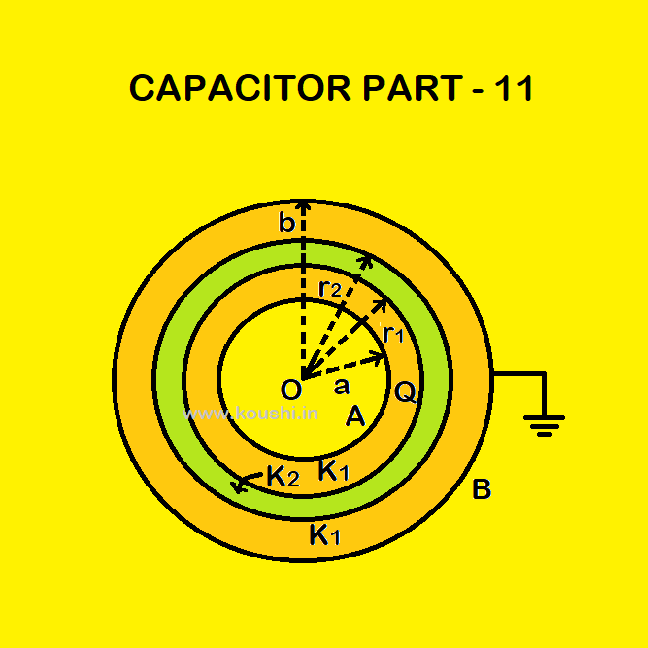
Capacitance of spherical capacitor with mixed dielectrics:
Let us consider A and B are the two concentric spherical shells of radii a and b respectively (b >a). Shell A is charged by Q and the outer surface of shell B is earthed.
Let a shell filled with dielectric medium of dielectric constant K2 of inner and outer radii r1 and r2 respectively as shown in figure. The remaining part of capacitor is filled with another dielectric medium of dielectric constant K1.
The electric field intensity in medium 1 of dielectric constant K1 at a distance r from the centre is 
 and that in medium 2 of dielectric constant K2 is 
.
As dV = – Edr, then for medium 1 dV = – dr and for medium 2 dV = – dr.
Then the potential difference between shell A and B is VB – VA = 
– dr + 
– dr + 
– dr
VA – VB = 
– dr + 
– dr + 
– dr
Or, VA – VB = 
[
 + 
[
 + [
Or, VA – VB = [ 
 – 
] + [Â – 
] + [ – 
]
Or, VA – VB = [ – ] – [ – ] + [ – ]
Or, VA – VB = 
Or, VA – VB = 
 
Or, VA – VB = [
]
Capacitance C = 
= 
 .
If K1 = 1 and K2 = K then, C = 
 .
If K1 = K2 = 1 then, C = 
is the Capacitance of spherical capacitor .
Force acting between the plates of the capacitor: Let us consider a parallel plate capacitor consists of two parallel plates each of plate area A are separated by a distance d. If F is force acting between two plates then
F = 
[see theory]
If V is the potential difference between the plates, then, V = Ed and F = 
.
If K is the dielectric constant between the plates, then, F = 
.
Click the button to go to the previous part of this chapter.