Bending of a cycle: When a cyclist moves on a curved road of radius r with sped v, he bends slightly at angle θ from his vertical position towards the inner side of the curve. m is the combined mass of the cycle and cyclist. The reaction force (R) offered by the road makes angle θ with vertical. Resolving R into two components, we get
(i) Rcos
which is equal to the weight of the system.
So, Rcos = mg ——(i)
(ii) Rsin which is directed towards the centre of the circular path and provides necessary centripetal force 
.
So, Rsin = —-(ii)
Dividing equation (ii) by equation (i) we get, 
= 
So, tan = 
.
Motion of a car on circular level road: Let us consider a car of mass m is moving with a constant speed v on a flat horizontal circular road of radius r. The normal reaction force offered by the road on the car in the upward direction is R = mg.
As the car is moving in the circular path, the necessary centripetal force provides by the frictional force f between the tyres of the car and road.
So, = f = µR = µmg where µ is the coefficient of friction.
v = 
.
Banking: During circular motion of a vehicle, to avoid accident the outer edge of the circular track is slightly increased than the inner edge. This is known as banking of curved track. The angle through which the outer edge is raised above the inner edge is called the angle of banking.
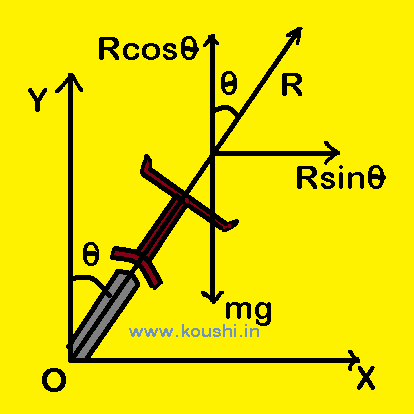
Motion of a car on circular banked road (frictionless): Let us consider a car of mass m is moving with a constant speed v on a circular banked road of radius r. The angle of banking is θ. The normal reaction force R acts along normal to the banked track. Resolving R into two components,
(i) Rcos which is equal to the weight of the car. So, Rcos = mg —(i)
(ii)Rsin which is directed towards the centre of the circular path and provides necessary centripetal force . So, Rsin = —-(ii)
Dividing equation (ii) by equation (i) we get, =
Or, tan =
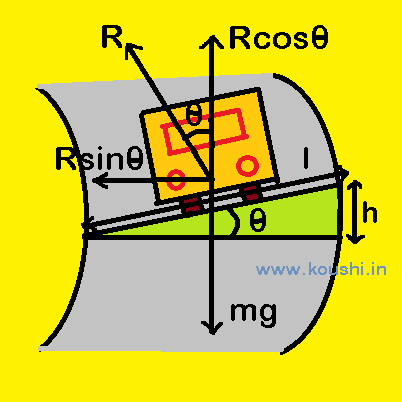
Or, v = 
.
When θ is very small, tan = sin = 
. Where h = height of the outer side with respect to the inner side and l is the length of the road.
v = .
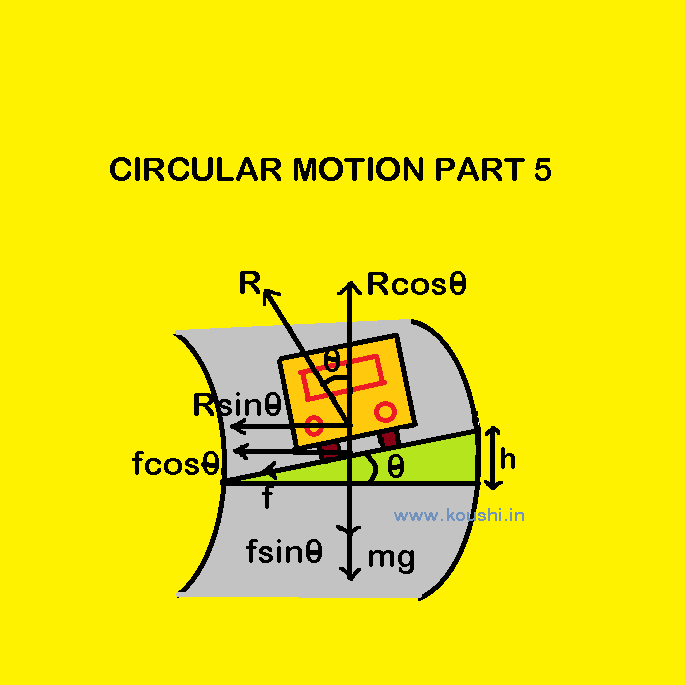
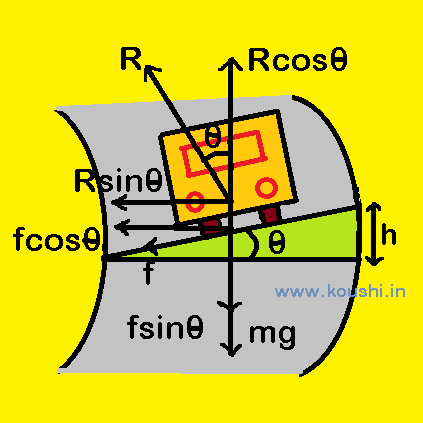
Motion of a car on circular banked road (with friction): Let us consider a car of mass m is moving with a constant speed v on a circular banked road of radius r. The angle of banking is θ. The frictional force f between the tyres of the car and road having two components. fcos is the horizontal component towards the centre of the track and fsin is the vertical downward component. f = µR where µ is the coefficient of friction. The normal reaction force R acts along normal to the banked track. Resolving R into two components, Rcos is along vertically upwards and Rsin is along horizontal towards the centre of the circular path.
The net horizontal components provide necessary centripetal force .
So, Rsin + fcos = —–(i)
The car does not have any vertical motion. So, mg + fsin = Rcos or, Rcos – fsin = mg —-(ii)
Dividing equation (i) by equation (ii) we get, 
=
Or, 
= [as f = µR]
Or, 
=
Or, 
=
v = 
.
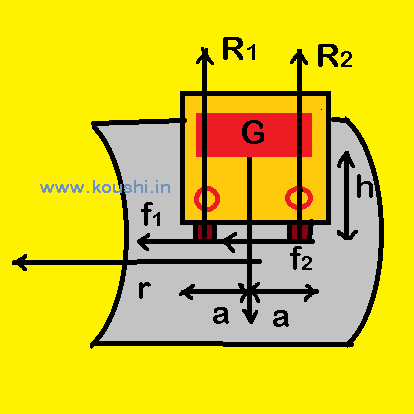
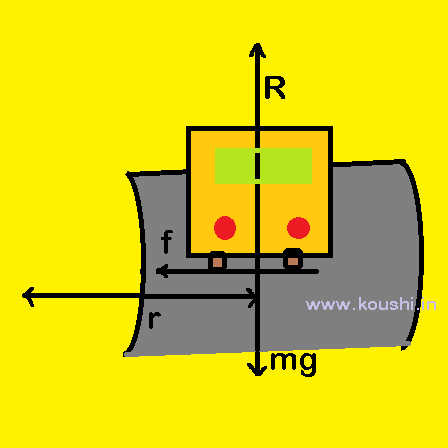
Condition of overturn of a car: A car of mass m moving on a horizontal circular track with speed v. The centre of mass of the car is at a height h from the road. The distance between the centre of mass of the car and the centre of the circlar road is r. The separation between the wheels is 2a. Find the limiting speed of the car not to overturn.
We consider the rear view of the car. The normal reaction of road on inner and outer wheels are respectively R1 and R2 therefore, R1 + R2 = mg ——- (i)
The frictional forces acting on the wheel provides the required centripetal force for rotation.
So, f1 + f2 = —- (ii)
Taking moment about the centre of mass G we get,
(f1 + f2)h + R1a – R2a = 0 [for rotational equilibrium net torque is zero]
Or, R2 – R1 = 
(f1 + f2) = 
——- (iii)
From equations (i) and (iii) we get, R1 = 
(mg – ) and R2 = (mg + )
Therefore, the inner wheel will leave the ground when R1 = 0.
The limiting speed of the car not to overturn is v = 
.
