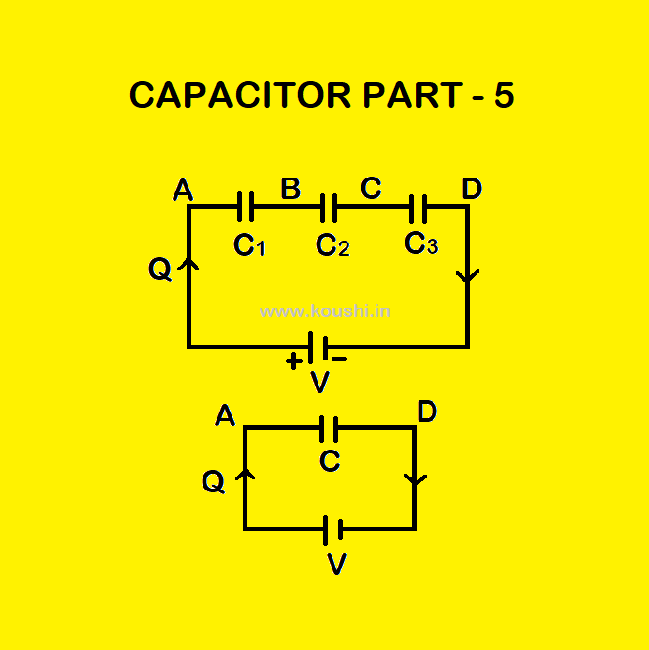
1. Capacitors in series: Let us consider three capacitors C1, C2 and C3 respectively are connected in series in between points AB, BC, CD with a cell as shown in figure. The potential difference between points AB, BC, CD are respectively (VA – VB), (VB-VC) and (VC-VD). Q is the charge flows through the circuit. Then we get,
VA – VB = ![]() ——-(1)
——-(1)
VB – VC = ![]() ——-(2)
——-(2)
VC – VD = ![]() ——-(3)
——-(3)
Adding equations (1), (2) and (3) we get, VA – VD = Q(![]() ) ——–(4)
) ——–(4)
If we substitute all capacitors C1, C2 and C3 by a single capacitor with capacitance C, keeping potential difference between points A and D same and Q is the charge flows through the circuit, then VA – VD = ![]() ——-(5).
——-(5).
From equations (4) and (5) we get, ![]() =
= ![]() .
.
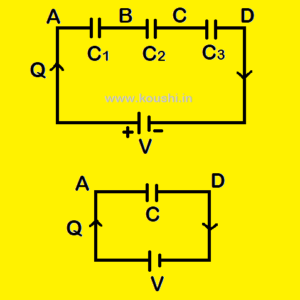
2. Capacitors in parallel: Let us consider three capacitors C1, C2 and C3 respectively are connected in parallel in between points A and B with a cell as shown in figure. The potential difference between points A and B is (VA – VB) = V. Q is the charge flows through the circuit and the charge through the capacitors C1, C2 and C3 are respectively Q1, Q2 and Q3, then, Q = Q1 + Q2 + Q3 or, Q1 = C1V, Q2 = C2V and Q3 = C3V
So, Q = V[C1 + C2 + C3 ] ———(1)
If we substitute all capacitors C1, C2 and C3 by a single capacitance C, keeping potential difference between points A and B same and Q is the charge flows through the circuit, then VA – VB = V = ![]()
Or, Q = VC ——-(2)
From equations (1) and (2) we get, C = C1 + C2 + C3.
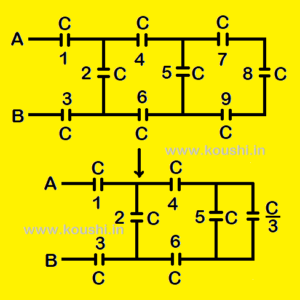
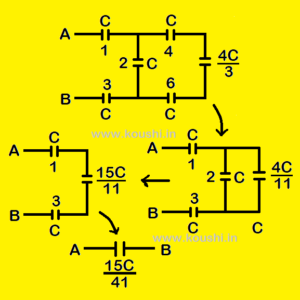
3. Finite ladder series:
Calculate equivalent capacitance between points A and B. To find the equivalent capacitance we have to start from the end as capacitors 7, 8 and 9 are connected in series. This combination is connected in parallel with capacitor 5. Again this process continues. At last capacitors 1, 3 and the equivalent of other capacitors (except capacitors 1and 3) are connected in series in between points A and B.
The equivalent of capacitors 7, 8 and 9 are connected in series is C/ = ![]() .
.
The equivalent of capacitors 5 and C/(= ![]() ) are connected in parallel is C//=
) are connected in parallel is C//= ![]() .
.
The equivalent of capacitors 4, 6 and C//(= ![]() ) are connected in series is C/// =
) are connected in series is C/// = ![]() .
.
The equivalent of capacitors 2 and C///(= ![]() ) are connected in parallel is C////=
) are connected in parallel is C////= ![]() .
.
The equivalent of capacitors 1, 3 and C//// (= ![]() ) are connected in series is Ceq=
) are connected in series is Ceq= ![]() .
.
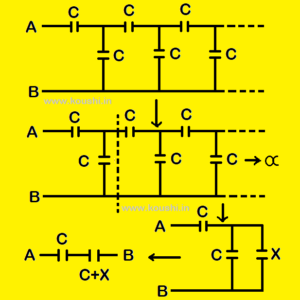
4. Infinite ladder series:
Calculate equivalent capacitance between points A and B. Let us consider the equivalent capacitance between A and B is x. Since the network consists of infinite number of capacitors, we can add or remove some capacitors which don’t change the net capacitance. For this purpose we have to follow the pattern of the network. So, ![]() = x
= x
Or, C2 + Cx = 2Cx + x2
Or, x2 + Cx – C2 = 0
Or, x = ![]()
Or, x = ![]()
So, x = ![]() .
.
[As the value of capacitance can’t be negative we ignore the term ![]() ].
].
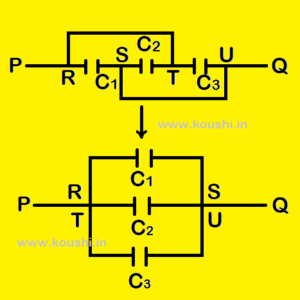
5. Same potential concept:
Calculate equivalent capacitance between points P and Q. If two points are connected with a conducting wire without capacitor then those points have same potential and those points can be considered as a single point. To calculate equivalent capacitance between points P and Q, we can consider points U and S are of same potential, therefore those points are considered as single point. Similarly points R and T also same point.
So all the capacitors are connected in parallel between points P and Q.
If C1 = C2 = C3 = C then Ceq = 3C.
Click the button to go to the next part of this chapter.
Click the button to go the previous part of this chapter.