Electric charges and field Part – 4
1. Concept of electrostatic force:
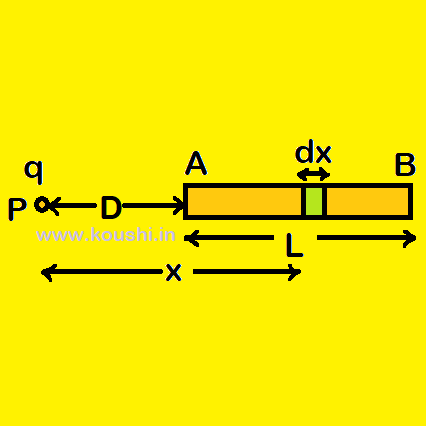
1. Force on a point charge due to uniformly charged rod: A rod of length L is uniformly charged by Q placed at a distance D from a point charge q at P. Charge per unit length of the rod is λ = 
. We consider an elementary part of the rod of length dx at a distance x from P. The charge of dx is dQ = dx.
The electric field at P due to dQ is dE = k(
)dx.
So, the total electric field at P due to the entire rod is
E = 
dE = 
= 
= 
= 
The force on charge q is F = qE = 
.
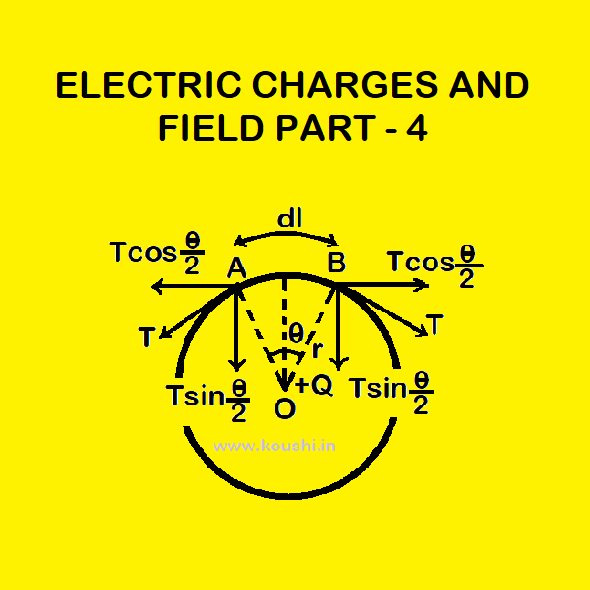
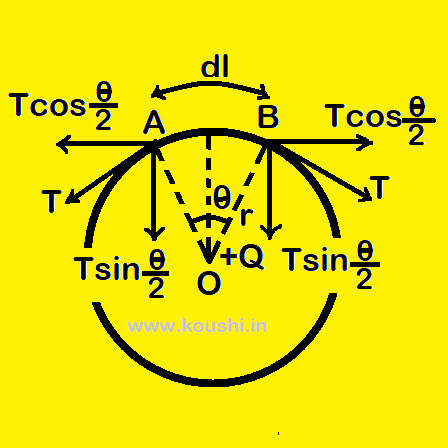
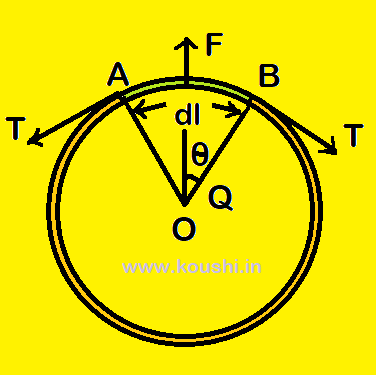
2. Tension on a charged ring: A circular ring of radius r is uniformly charged by q, so the charge per unit length is λ = 
. AB is the elementary part of the ring of length dl with charge dq = λdl = 
. A point charge Q is placed at the centre O of the ring.
The force on AB due to Q is dF = 
= 
.
Let T is the increase in tension on the ring to balance the repulsive force. The inward tension for the part AB is 2Tsin
.
As θ is very small then, from figure 
= or, dl = rθ.
Then, 2Tsin =
Or, 2T =
Or, T
=
T = 
.
3. Increased radius of the ring due to excess tension: Let us consider 
r is the increased in radius of the ring due to excess tension. So, increased in length of the ring is 
(r + r) – 2πr = 2π∆r.
Therefore strain = 
= 
. Stress = 
where A is the cross-sectional area of the ring.
If Y is the Young’s modulus of the material of the ring then, Y = 
= 
Or, r = 
= 
[F = ].
4. Vertical circular motion of a charged ball: A ball of mass m charge q is tied at one end of an insulated thread of length L. The other end of the thread is connected with a fixed charge -Q. The minimum horizontal speed is required at the top point of the vertical circular motion of the ball is u. The electrostatic force between two charges is F = 
.
The force on the ball at an angle θ with vertical is T + F – mgcos
= 
v2
Where T is the tension of the string and v is the speed at that instant.
At the top most point T = 0 and θ = 1800 so, u2 = F + mg or, u =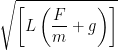 
If the minimum tangential speed at the lowest point is v then, 
mu2 + mg2L = mv2
Or, mv2 = m[L( 
+ g)] + 2mgL
Or, v =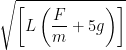 
.
Tension at the lowest point is T = v2 + mg – F = 6mg.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.
tag:
Share:
Admin Koushi
