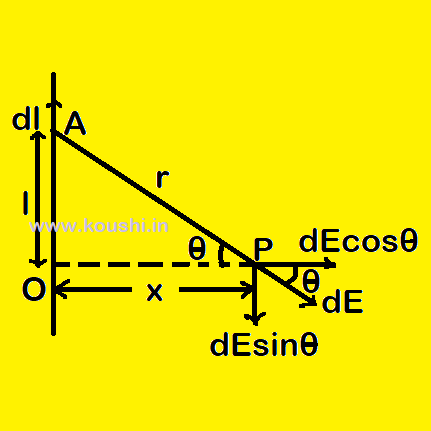
Electric field intensity of a uniformly charged infinitely long thin wire:
Let us consider a long thin wire having uniformly positive linear charge density λ. We consider the elementary length dl of the wire carry small charge dq = λdl at a distance l from point O of the wire. The magnitude of the electric field of dq produced at point P at perpendicular distance x from O is dE = 
= 
———(i) and is directed along the line AP.
If we resolute dE, the vertical component i.e. dE
is cancelled due to the effect of elementary charge dq at the same distance l bellow O. So the horizontal component i.e. dE
provides the electric field at point P due to the elementary charge dq.
So the net electric field at point P due to the uniformly charged wire is
E = 2
dE = 2
——–(ii) [2 is due to the two halves of the wire make the same contribution]
From figure, r = x
and l = x
So, dl = x
——(iii)
From equation (ii) and (iii) we get, E = 
For infinitely long thin wire E = 2k
= 
= 
Where k = 
and 
= 
= sin
– sin00 = 1.
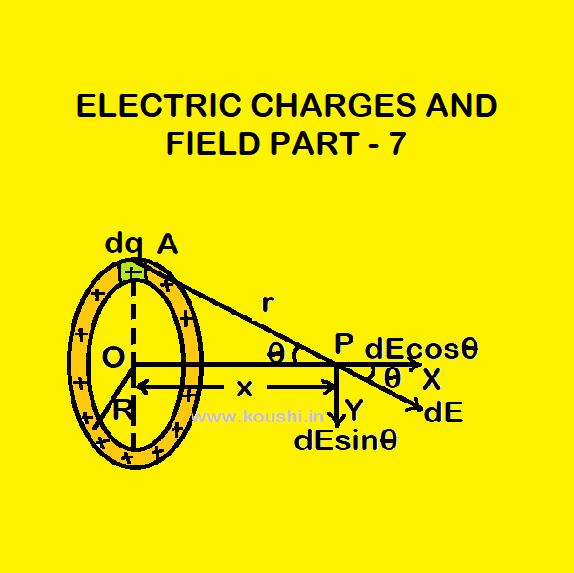
Electric field intensity due to a uniformly charged ring:
Let us consider a ring of radius R having uniformly positive linear charge density λ. We consider the elementary length dl of the wire at point A carry small charge dq = λdl. The magnitude of the electric field of dq produced at point P at a distance x on the axis from the centre of the ring O is dE = = —–(1) and is directed along the line AP. If we resolute dE, the vertical component i.e. dE (along PY) is cancelled due to the effect of elementary charge dq at the opposite side of the ring. So the horizontal component i.e. dE (along PX) provides the electric field at point P due to dq.
So, the net electric field at point P due to the uniformly charged wire is E = dE
Or, E = 
where cosθ = 
Or, E = 
= 
[where r = 
]
Where k = so, E = 
.
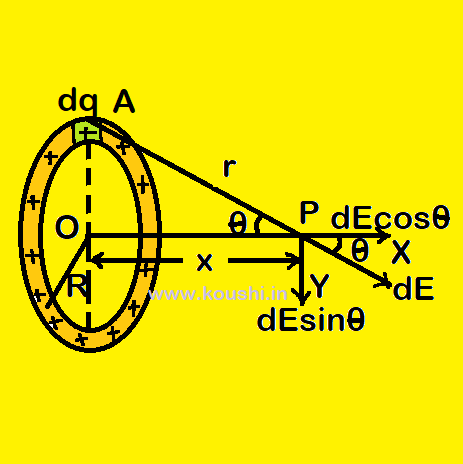
Electric field intensity due to a uniformly charged ring is E = 
.
(i) At x = 0, E = 0, so charges on opposite sides of the ring apply force in opposite directions on a test charge at the centre, and the net force on it is zero.
(ii) When x 
R then E = 
so its field is the same as that of a point charge.
(iii) For the position where E is maximum is 
= 0. So, 
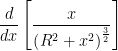= 0
Or, 
= 0 or, 3x2 = x2 + R2 x = 
.
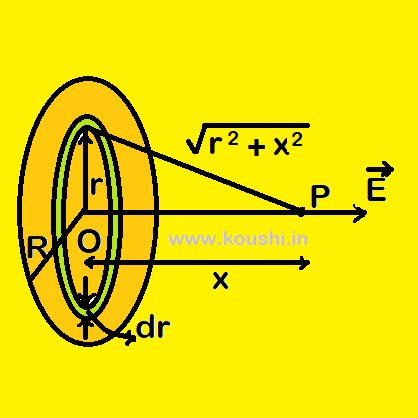
Electric field intensity due to a uniformly charged disc:
Let us consider a disc of radius R having uniformly positive surface charge density σ. We consider the elementary ring of the disc of radius r and thickness dr about the axis. The elementary ring carries small charge dq = σ2πrdr. The magnitude of the electric field of the elementary ring produced at point P at a distance x on the axis from the centre of the ring O is
dE = 
= 
———-(1)
Clearly, E = 
= 
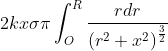
Let us consider, r2 + x2 = z2 or, rdr = zdz
So,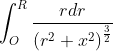 
= 
= 
= 
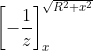So, E =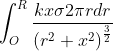 
= 
Where k = 
and q = σπR2 so, E = 
.
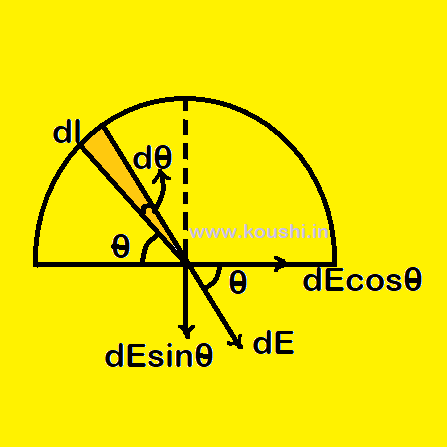
Electric field intensity at the centre of a uniformly charged semicircular ring:
Let us consider a semicircular ring of radius r having uniformly positive linear charge density λ. We consider the elementary length dl of the ring carry small charge dq = λdl at an angle θ with X axis.
The magnitude of the electric field due to dq produced at centre of the ring O is dE = 
= 
———(1)
The horizontal component i.e. dEcos
is cancelled due to the effect of elementary charge dq at the opposite side of the ring. The vertical component i.e. dEsin provides the electric field at centre due to dq.
So, the net electric field at centre due to the uniformly charged semicircular ring is
E = 
E = 
where dl = rdθ and k =
E = 
= 
= 
.
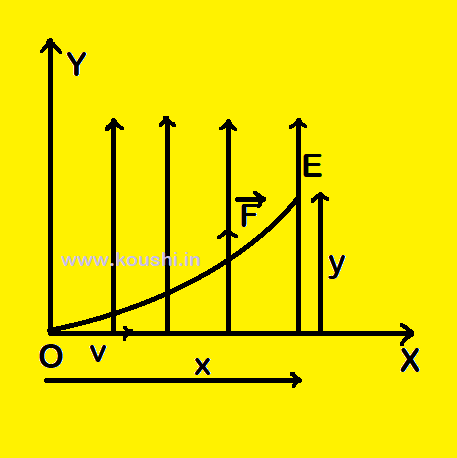
Motion of a charge perpendicular to uniform electric field:
Let us consider a point charge q of mass m is moving along +ve x axis with uniform speed v and uniform electric field of intensity E is acting along +ve y axis. The component of speed of the charge along +ve y axis is vcos900 = 0, so the charge is rest in electric field. Therefore the force acting on the charge is F = qE and the acceleration of the charge is a = 
.
The distance travelled by the charge along +ve y axis with acceleration a for time t is y = 
at2 = 
—– (i)
The distance travelled by the charge along +ve x axis with uniform speed v for time t is x = vt ——— (ii)
From equations (i) and (ii) we get, y = 
.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.