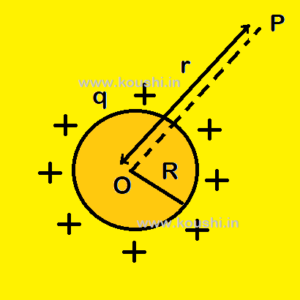
1. Electric potential due to uniformly charged spherical shell: Let us consider a spherical shell of radius R is charged by q. Calculate electric field at a point P, at a distance r from the centre of the shell.
(i) If point P is outside the shell then potential at P is V = 
.
(ii) If point P is on the surface of shell then potential at P is V = 
.
(iii) If point P is inside the shell or at the centre of the shell then potential at P is V = .
[Inside the spherical shell E = 0, therefore, – 
 = 
 = 0 or, VS – V = 0 
 V = VS].
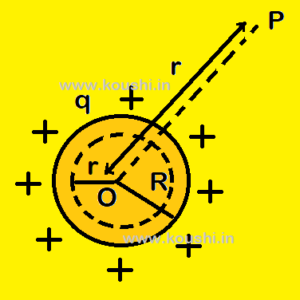
2. Electric potential due to uniformly charged solid sphere: Let us consider a solid sphere of radius R is charged by q. Calculate electric field at a point P, at a distance r from the centre of the sphere.
(i) If point P is outside the sphere then potential at P is V = .
(ii) If point P is on the surface of sphere then potential at P is V = .
(iii) If point P is inside the sphere then using Gauss’s law the electric field E = 
.
Now dV = -Edrcos00 = – dr or, V = 
= – 
Or, V – = – 
[r2 – R2]
Or, V = [1 + 
 – 
] = [
– ].
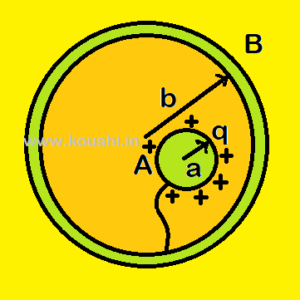
3. Concept on potential due to shearing of charge: A solid sphere (A) of radius a is charged by q and its potential is VA = 
. Now the sphere is connected with a hollow sphere (B) of radius b using a conducting wire. Now the charge will reside on the outer surface of B [using Gauss’s law].
The potential of B is VB = 
. As the sphere A is inside the sphere B, now the potential of sphere A is 
= = 
 = 
VA.
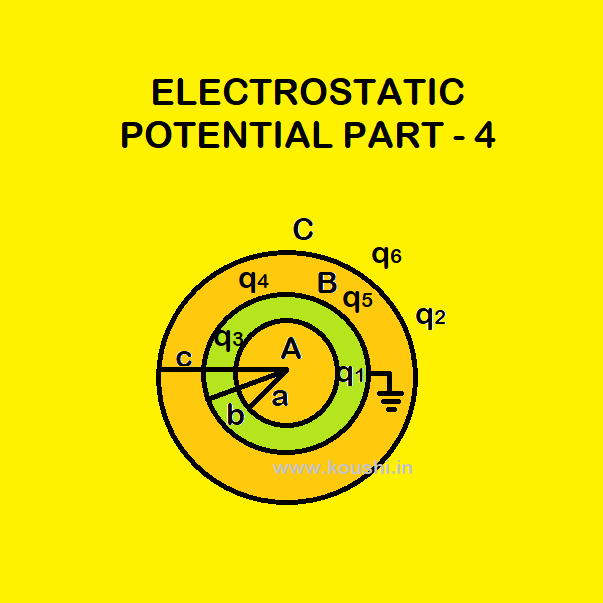
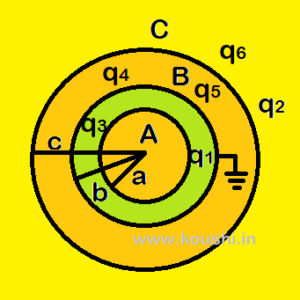
4. Charge appears on different surfaces: Let us consider three spherical shells A, B and C of radii a, b and c respectively. Shell B is grounded and shell A and C are charged by q1 and q2.
As q1 charge remain on outer surface of shell A then no charge is on the inner surface of it.
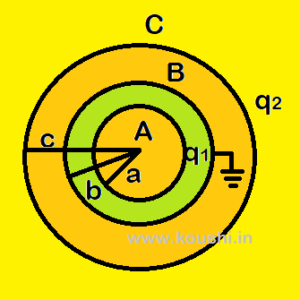
Let q3 and q4 are the charge of inner and outer surface of shell B respectively. Using Gauss’s law through the material of B we get, q3 = – q1.
Let q5 and q6 are the charge of inner and outer surface of shell C. Using Gauss’s law through the material of C we get, q5 = – q4. So, q2 = q5 + q6.
As the potential of shell B is 0 then k[
 + 
 + 
] = 0.
Using these conditions charge of different surfaces can be calculated.
Click the button to go to the previous part of this chapter.