Electric flux: The electric flux through a surface inside an electric field is the total number of electric lines of force crossing the surface in a direction normal to the surface.
If E is the electric field creates angle θ with surface of elementary area dS then electric flux, dɸE = EdScosθ
Or, dɸE = 
.
Then total electric flux through the surface is ɸE = 
..
Gauss’s theorem: The surface integral of the electric field intensity over any closed hypothetical surface (Gaussian surface) in free space is equal to the 
times the net charge enclosed within the surface. ɸE = . = 
.
Let us consider a charge q is situated at the centre O of the sphere of radius r. If E is the electric field at any point on the sphere, then E = 
. Let us consider elementary surface area dS on the sphere.
The electric flux through the elementary surface dɸE = . = EdScos00 = EdS.
The total flux through a surface of sphere ɸE = 
dɸE = EdS = E4πr2 = 
= .
Deduction of Coulomb’s law from Gauss’s law:
Let us consider a point charge Q placed at O. To calculate electric field at point P due to this point charge, we consider a Gaussian sphere of radius R. From Gauss’s law 
. = 
Or, 
.
=
Or, E = 
If another charge q is placed at point P then, the electrostatic force acting between the charges is F = qE = 
. This is Coulomb’s law.
Electric field due to a uniformly charged infinite plane sheet: Let us consider AB is a flat thin sheet with uniform surface charge density σ. Let us consider S is an elementary area of the sheet. To enclose S we consider a cylindrical Gaussian surface with two plane surfaces S1 and S2 (each of area S) and curve surface S3. Since the sheet is infinite, by symmetry, the magnitude of field E at points P and P’, equidistance from the sheet in opposite side are same. Let flux through S1, S2, S3 are respectively ɸ1, ɸ2, ɸ3.
ɸ1 = 
= 
= ES 
ɸ2 = 
= 
= ES
ɸ3 = 
= 0 
Using Gauss’s theorem we get, total flux through the Gaussian surface ɸ = ɸ1 + ɸ2 + ɸ3 = ES + ES + 0 = 2ES
i.e. 2ES = 
so, E = 
(q is the charge enclosed within the Gaussian surface.)
Or, E = 
[where 
is the surface charge density].
Electric field due to a uniformly charged straight wire: Let us consider a thin infinitely long wire with uniform linear charge density λ.
To calculate the electric field at a distance r from it, we consider a coaxial Gaussian cylinder of radius r and length l consist of two plane surfaces S1 and S2 (each of area S) and curve surface S3. Let flux through S1, S2, S3 are respectively ɸ1, ɸ2, ɸ3. By symmetry, the field must have the same magnitude E and directed normally outward.
ɸ1 = 
. = 0 ( ⊥
)
ɸ2 = 
. = 0 ( ⊥ )
ɸ3 = 
. = E.dS = ES = E2πrl ( 
)
Using Gauss’s theorem we get, total flux through the Gaussian surface ɸ = ɸ1 + ɸ2 + ɸ3 = ES = E2πrl
i.e. 2Eπrl = so, E = 
= 
(q is the charge enclosed within the Gaussian surface.)
Electric field due to a uniformly charged solid sphere:
1)Inside sphere: Let us consider a solid sphere of radius R with uniform volume charge density ρ. To calculate the electric field at a distance r from the centre (r < R ), we consider a spherical Gaussian surface of radius r. By symmetry, the field must have the same magnitude E and directed normally outward over the Gaussian surface.
So, 
= 
= ES = E4πr2 ——-(i)
The charge enclosed within the Gaussian surface q’
= volume of the sphere of radius r 
ρ = 
πr3ρ
If q is the charge enclosed within the solid sphere then ρ = 
i.e. q’ = 
——–(ii)
Using Gauss’s theorem we get, = 
Or, E4πr2 = 
E = 
[from equations (i) and (ii)].
2) Outside sphere: Let us consider a solid sphere of radius R with uniformly charged by q. To calculate the electric field at a distance r from the centre (r > R ), we consider a spherical Gaussian surface of radius r. By symmetry, the field must have the same magnitude E and directed normally outward over the Gaussian surface.
So, = = ES = E4πr2
Using Gauss’s theorem we get, = = 
Or, E4πr2 =
E = 
.
3) On the surface of sphere: Let us consider a solid sphere of radius R with uniformly charged by q. To calculate the electric field at a point on the surface of sphere, we consider a spherical Gaussian surface of radius R. By symmetry, the field must have the same magnitude E and directed normally outward over the Gaussian surface.
So, = 
= E4πR2
Using Gauss’s theorem we get, =
Or, E4πR2 =
E = 
.
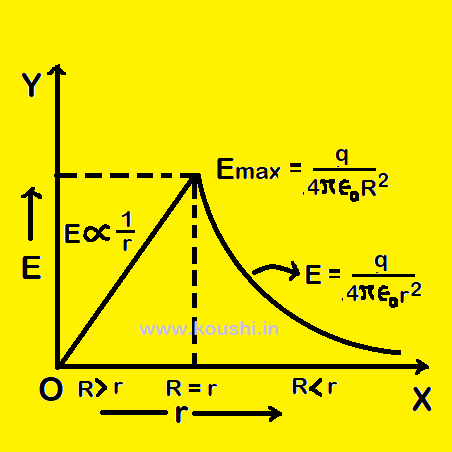
The variation of electric field with distance of a uniformly charged solid sphere is given.
Electric field due to a uniformly charged hollow sphere or thin spherical shell:
1) Inside sphere: Let us consider a hollow sphere of radius R with uniform charge q. To calculate the electric field at a distance r from the centre (r < R ), we consider a spherical Gaussian surface of radius r. As charge remain outside the surface of the sphere then no charge is enclosed by the Gaussian surface.
So, = 0 or, E = 0.
2) Outside sphere: Let us consider a hollow sphere of radius R with uniformly charged by q. To calculate the electric field at a distance r from the centre (r > R ), we consider a spherical Gaussian surface of radius r. By symmetry, the field must have the same magnitude E and directed normally outward over the Gaussian surface.
So, = = ES = E4πr2
Using Gauss’s theorem we get, = =
Or, E4πr2 =
E = .
3) On the surface of sphere: Let us consider a hollow sphere of radius R with uniformly charged by q. To calculate the electric field at a point on the surface of sphere, we consider a spherical Gaussian surface of radius R. By symmetry, the field must have the same magnitude E and directed normally outward over the Gaussian surface.
So, = = ES = E4πR2
Using Gauss’s theorem we get, =
Or, E4πR2 =
E = .
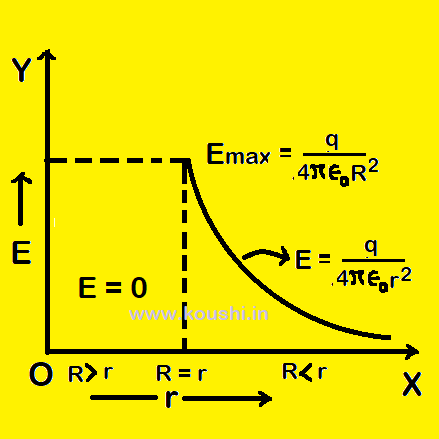
The variation of electric field with distance of a uniformly charged spherical shell is given.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.