Laws of motion
LAWS OF MOTION
Newton’s first law: Every body persists in its state of rest or of uniform motion in a straight line unless it is compelled to change that state by external force on it.
From Newton’s first law, we get definition of force and inertia.
Force: Force is the push or pull which changes or tends to change the state of rest or of uniform motion in a straight line.
Inertia: This is the property by virtue of which a body tends to resist the change of its state of rest or of uniform motion in a straight line.
Inertia of rest: This is the property by virtue of which a body maintains its state of rest or tends to remain at rest.
Passengers sitting in a bus experience jerk in the backward direction when the bus suddenly starts moving. When the bus suddenly starts moving the lower part of the passengers share the motion but the upper part tends to remain at rest due to inertia of rest.
Inertia of motion: This is the property by virtue of which a body maintains its state of uniform motion or tends to maintain its motion.
Passengers standing in a moving bus experience jerk in the forward direction when the bus suddenly stops. When the bus suddenly stops the lower part of the passenger comes to rest but the upper part remains in the state of motion on account of inertia of motion.
Newton’s second law: The time rate of change of momentum of a body is directly proportional to the impressed force and takes place in the direction of the force.
Prove F = ma: Let us consider a body of mass m is moving with uniform velocity u.
Then it accelerates uniformly with a and after time t its final velocity is v.
The initial momentum of the body = mu and final momentum of the body = mv.
So, the change in momentum of the body = mv-mu.
According to Newton’s second law,
Applied force, F 
Or, F = 
(where k = constant)
Or, F = kma (v = u+at)
If one unit force is applied on a unit mass to produce unit acceleration, then k = 1. If k = 1, then F = ma.
Absolute unit of force:
C.G.S. unit is dyne (1 dyne = 1g 1cms-2). One dyne of force is the amount of force required to accelerate a body with 1 cms-2 of mass 1 gram.
SI unit is newton (1 newton = 1Kg 1ms-2). One newton of force is the amount of force required to accelerate a body with 1
ms-2 of mass 1Kg.
1N = 1Kg 1ms-2 or, 1N = 103 g 102cms-2 or, 1N = 105 gcms-2 or, 1N = 105 dyne.
Gravitational unit of force:
C.G.S. unit is gram-weight (gwt). One gram weight is the force with which a body of mass 1g is accelerated towards the centre of earth. 1gwt = 1g 981cms-2 = 981 dyne.
SI unit is kilogram-weight (kgwt). One kilogram weight is the force with which a body of mass 1Kg is accelerated towards the centre of earth. 1Kgwt = 1Kg 9.81ms-2 = 9.81 newton.
Dimension of force: F = ma, [F] = [MLT-2].
Impulse: The total effect of force is called impulse. It is the product of force and the time for which the force is applied.
Let us consider a body of mass m is moving with uniform velocity u. Then it accelerates uniformly with 
and after time t its final velocity is 
. The applied force,
= 
or, = .
The impulse 
= .t = = m(
– 
) = m – m = change of momentum of the body.
If the force is applied for time interval t1 to t2 then impulse = 
dt .
Impulsive force: When a heavy amount of force is applied on a body for a small interval of time to change of momentum of the body then that force is called impulsive force. Example: Collision between bat and ball.
Balance force: If the resultant force of all the forces acting on a body is zero, then those forces are called balance force.
Unbalance force: If the resultant force of all the forces acting on a body is nonzero, then those forces are called unbalance force. For unbalance force, resultant force = mass × acceleration.
Newton’s third law: To every action, there is always an equal (in magnitude) and opposite (in direction) reaction.
Law conservation of linear momentum: If the vector sum of the external forces acting on a system is zero, then the total momentum of the system is conserved i.e. remain constant.
Let us consider two bodies A and B of masses m1 and m2 are moving with initial velocity 
and 
( > ) in the same direction and after some time they collide and move in the same direction with final velocity 
and 
( < ) respectively.
The change in momentum of the body A = m1( – ) and the change in momentum of the body B = m2( – ).
If the collision time is t, and 
is the action of B on A and 
is the action of A on B, then from Newton’s third law,
= –
Or,t = – t —–(i).
The impulse of body A =t = m1( – )and impulse of body B = t = m2( – ).
Then from equation (ii) we get, m1( – ) = – m2( – )
Or, m1 – m1 = – m2 + m2
Or, m1+ m2 = m1 + m2 .
So, the momentum of the system before collision = the momentum of the system after collision.
Recoil of gun: Let us consider, initially the gun and bullet are rest. So, the momentum of the system before firing is zero.
Let m = mass of bullet, M = mass of gun, = velocity of bullet, 
= velocity of gun after firing. As there is no external force is applied then the total momentum of the system is conserved.
So, from conservation of linear momentum, 0 = m +M
Or, = – 
[– ve sign indicates that the motion of gun is opposite to that of bullet.]
Concepts to solve numerical based on Newton’s law:
(i) Consider a system on which laws of motion are to be applied. It may be a body or a point mass or a single block or the combination of blocks.
(ii) After identifying the system, consider all the forces acting on the system. Ignore the forces which are applied by the system on other body.
(iii) If the forces are coplanar then resolute all the forces along x axis and y axis.
(iv) If the body is in equilibrium, then 
= 
= 0. If the body is in motion, then = m
and = m
.
Concepts on Newton’s law:
- A ball of mass m is thrown perpendicularly on the wall with speed u and rebounces with speed v. The collision time of ball with wall is t. Find force on the ball by wall.
The momentum of the ball before collision with the wall is Pi =- mu [taking the direction of momentum along + ve x axis is positive.]
The momentum of the ball after collision with the wall is Pf = mv
Change of momentum P = Pf – Pi = mv – (- mu) = m(u+v)
Force on the ball by wall F =
[direction is along +ve x axis].
- A ball of mass m is thrown on the wall with speed u at an angle and rebounces with speed v at same angle as shown in figure. The collision time of ball with wall is t. Find force on the ball by wall.
Let us consider the direction of momentum along + ve x axis and + ve y axis are positive.
The momentum of the ball before collision with the wall is Pi = mu
Andresoluting it along x and y axis we get, Pix = – mu sin
and Piy = – mu cos .
The momentum of the ball after collision with the wall is Pf = mv and resoluting it along x and y axis we get, Pfx = mv sin and Pfy = – mv cos .
Change in momentum along x axis is Px = Pfx – Pix = mv sin – (- mu sin ) = m sin (u+v)
Change in momentum along y axis is Py = Pfy – Piy = – mvcos -(- mucos ) = mcos (u-v)
Net change in momentum P =
= 
Therefore, force on the ball by wall F 
= [direction is along +ve x axis].
- A stream of water flowing horizontally with a speed u gushes out of a tube of cross-sectional area A and hits a vertical wall nearby. Find the force exerted on the wall by the impact of water. [Assume water does not rebound]
Let us consider m mass of water hits the wall for time t.
So, m = volume of water flows for time t density of water
m = Area × distance travelled by water for time t × density of water
m = Aut
[density of water is ]
Momentum of water before collision with the wall [direction perpendicular to the wall] = mu = Au2 t
As the water does not rebound so after collision with wall, momentum of water is zero [mv = mucos900 = 0].
Therefore, force exerted on the wall by the impact of water is
F = 
= 
= 
.
- Concepts on free body diagram: (i) A uniform rope of length L, resting on a frictionless horizontal surface is pulled at one end by a force F. Find the tension in the rope at a distance l from the end where the force is applied.
Let us consider the mass of the rope is M and mass per unit length of the rope is 
.
So, the mass of the part of length l is m =
. Acceleration of rope is a = 
.
Considering the part of the rope of length l as a system the forces act on it are F and T
(T is tension applied on this part by the other part).
Then using Newton’s 2ndlaw we get, F -T = ma = 
∴ T = F – = 
.
(ii) Two bodies of mass M and m are connected by string and m mass is pulled by a force F on frictionless surface. Find tension acting along the string.
Consider two bodies as a system and F is the external force acting on the system.
So, the acceleration of the system is a = 
.
Now consider the body of mass m as a system and F and T (tension) act on the body.
The net force acts on it is 
= F -T = ma [as the acceleration is directed along the direction of external force F, so F > T]
Or, T = F – ma = F – 
= 
.
If we consider the body of mass M as a system and T is the external force acts on it by mass m then T = Ma = 
.
- Concept on action reaction force: A sphere of weight w is resting on a V-groove as shown in figure. Let us consider N1 and N2 are the normal reaction forces act on the sphere by the sides of V-groove then,
+ 
=
.
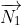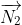Example: A homogeneous sphere of mass m rests on an inclined plane A of inclination and against the vertical wall B as shown in figure. All the surfaces are frictionless. Find the reaction forces acting on the sphere by the surfaces.
Let us consider, N and R are the reaction forces act on sphere from surface A and B respectively. After resolution of N and R we get, Ncos = mg —— (i) and R = Nsin —– (ii)
Dividing equation (ii) by equation (i) we get, R = mgtan .
From equation (ii) we get, N =
= 
= mgsec .
- A rod P remain always perpendicular to the surface of a wedge Q by fixing two supports as shown in figure. Al the surfaces are frictionless. If the masses of rod and wedge are respectively m and M, then find their acceleration.
Let us consider, the displacement of the rod is AB = xP and displacement of the wedge is AC = xQ.
From triangle ABC, AB = ACsin or, xP = xQsin —– (i)
Double differentiating equation (i) with respect to time we get, aP = aQsin —– (ii)
The action reaction force between rod and wedge is N.
Using free body diagram for rod and wedge we get, mgcos – N = maP —– (iii)
Nsin = MaQ—— (iv)
From equation (ii) and (iii) we get, mgcos – N = maQsin —— (v)
From equation (iv) and (v) we get, (mgcos – maQsin )sin = MaQ
∴ aQ = 
And aP = aQsin = 
.
Lami’s theorem: If three forces acts on a particle to maintain equilibrium, then we get the relation of those forces by Lami’s theorem. Lami’s theorem states that the ratio of one side of a triangle to the sine of its opposite angle remain constant.
From diagram using Lami’s theorem, 
= 
= 
.
Example: A particle O is in equilibrium due to influence of three forces as shown in figure. Find the value of forces F1 and F2.
Using Lami’s theorem, 
= 
= 
So, = 4 or, F1 = 4sin
= 2 N.
= 4 or, F2 = 4sin
= 2
N.
Torque: Torque or moment of force required to give turning effect on a body. Torque is defined as the product of force and its perpendicular distance from the axis of rotation.
Torque or moment of force about point Q = Force at point P × Perpendicular distance QO
= F×QP sin = FR sin = RFsin
∴
= 
× . The direction of torque is perpendicular outward to the plane of and
[Place your palm on the plane of and rotate your fingers (except thumb) from the direction of to , then the direction of thumb indicates the direction of torque.]
(i) AB is a rod of length 2l and O is the centre of the rod. F1 and F2 are two forces act from point A and B respectively perpendicular to the rod as shown in figure. Find torque at point O.
The torque at point O due to F1 is 
= F1l [direction is perpendicular to the plane upward].
The torque at point O due to F2 is 
= F2l [direction is perpendicular to the plane upward].
So, net torque at point O is 
= + = (F1 + F2)l [direction is perpendicular to the plane upward].
(ii) AB is a rod of length 2l and O is the centre of the rod. F1 and F2 (F1 > F2) are two forces act from point A and B respectively perpendicular to the rod as shown in figure. Find torque at point O.
The torque at point O due to F1 is = F1l [direction is perpendicular to the plane upward].
The torque at point O due to F2 is = – F2l [direction is perpendicular to the plane downward and –ve due to downward direction].
So, net torque at point O is = + = (F1 – F2)l [direction is perpendicular to the plane upward].
A mass less rod AB of length 4l is pivoted at point O (middle point of the rod). Three forces F, F and 2F are applied on AB at point A,C and B as shown in figure. Find the torque acting on the rod about point O.
As 2F force is not perpendicular to AB, then the vertical component of force 2Fsin300 acts at point B, produce torque. The horizontal component of force 2Fcos300 acts at point B but there is no perpendicular distance between this force with respect to point O, therefore torque due to this fore about point O is zero.
So, the net torque at point O due to the forces is = – F.OA + F.OC + 2Fsin300.OB = – F2l + Fl + F2l = Fl [taking clockwise rotation is negative and anticlockwise rotation is positive].
When a body is in equilibrium condition or at rest or possess only translational motion, then net torque on the body is zero.
When a body rotates then net torque = moment of inertia × angular acceleration
Pulley related problem:
1.If the pulley is fixed then tension acts all the points on a string is same and acceleration of two bodies which are connected by that string also remain same.
Let us consider two blocks of mass M and m (M > m) are connected by a massless inextensible string over a fixed smooth pulley. Then tension acts on the string is T and two blocks move with acceleration a. Using free body diagram for block of mass M (considering M as a system) we get, Mg – T = Ma ——–(i)
[Here Mg is the force acts on the system by earth and T is the tension acts by string on the system, as M> m, M moves downward so, Mg >T and resultant force is downward hence acceleration is downward.]
Using free body diagram for block of mass m (considering m a system) we get, T – mg = ma ——–(ii)
[Here mg is the force acts on the system by earth and T is the tension acts by string on the system, as M > m, m moves upward so, T >mg and resultant force is upward hence acceleration is upward.]
From equation (i) and equations (ii) we get, a = 
and T = 
.
- Free pulley problem: i)If the pulley is free then tension acts all the points on a string is same and acceleration of two bodies or centre of pulley depends on the change of displacement. ii)Create an equation of total length of a string by using those displacement relation. iii)Differentiate the equation with respect to time to get acceleration.
Two blocks 1 and 2 of mass m and M respectively are connected by strings with three pulleys as shown in figure. Find the relation between the acceleration of two bodies. Taking upward motion is positive calculate tension of blocks 2and acceleration of block 1.
Pulley 3 is a fixed pulley and we draw a horizontal reference line from the centre of the pulley. The displacement of blocks 1, 2 and pulley 3 and 4 are respectively x1, x2, x3 and x4.
Now, x1 + x4 = l1—– (i) [l1 is the length of the string passing over pulley 3]
(x1 – x4) + (x5 – x4) = l2or, x1 – 2x4 + x5 = l2—– (ii) [l2 is the length of the string passing over pulley 4]
(x1 – x5) + (x2 – x5) = l3 or, x1 – 2x5 + x2 = l3 —– (iii) [l3 is the length of the string passing over pulley 5]
Double differentiating equation (i) we get, a1 + a4 = 0 ——-(iv) [as the length of the string is constant so differentiation of length is zero]
Similarly, a1 – 2a4 + a5 = 0 —– (v)
And a1 – 2a5 + a2 = 0 —— (vi)
After solving equation (iv), (v) and (vi) we get, a2 = – 7a1.
Let us consider, tension of block 2 is T and it is moving downward and block 1 is moving upward with acceleration a. Using free body diagram of blocks 1 and 2 we get, for block 2, Mg – T = Ma2= 7Ma [a2 = – 7a1] —— (vii)
For block 1, T + T1 + T2 – mg = ma [a1 = a]
T + 2T + 4T – mg = ma [T1 = 2T, T2 = 2T1]
7T – mg = ma —— (viii)
From equation (vii) and (viii) we get, a = 
and T = 
.
- A man of mass M is standing on a massless weighing machine which is kept in a box of mass m. The box is hanging by a massless inextensible rope over a fixed pulley as shown in figure. The other end of the rope is held by the man. Find the force should he exert on the rope so that he gets his correct weight on the machine.
To solve this problem, we have to calculate the reading of weighing machine when the man manages to keep the box at rest. In this case if the man applied downward force F on the rope, then the tension on the rope T = F —- (i).
Using free body diagram for man we get, R + T = Mg ——– (ii)[R is the reading on the weighing machine]
Using free body diagram for weighing machine we get, R = N ——- (iii) [where N is the action reaction force between weighing machine and box.]
Using free body diagram for box we get, T = N + mg —– (iv)
From equation (iii) and (iv) we get, T = R + mg —– (v)
From equation (ii) and (v) we get, Mg – R = R + mg
Or, R = 
.
This signifies that if the box is rest then the reading is less than Mg. Therefore, the man should apply sufficient force on the rope so that the box can accelerate upwards and the reading shows on the weighing machine is
R = Mg.
Now, if the man applied downward force F/ on the rope, then the tension on the rope T = F/ —- (i).
Using free body diagram for man we get, R + T – Mg = Ma [R is the reading on the weighing machine and a is the acceleration of the box.]
Or, Mg + T – Mg = Ma
Or, T = Ma ——– (ii)
Using free body diagram for weighing machine we get, R = N ——- (iii) [where N is the action reaction force between weighing machine and box.]
Using free body diagram for box we get, T – N – mg = ma —– (iv)
From equation (iii) and (iv) we get, T – R – mg = ma
Or, T – Mg – mg = ma
Or, Ma – Mg – mg = ma [using equation (ii)]
Or, a = 
—– (v)
Therefore, T = F/ = Ma = 
.
Spring force: When a spring is compressed or elongated by a force F and the elongation or compression is x, then
F 
x or, F = kx [where k is the force constant of a spring] —-(1)
Potential energy stored in a spring: When a spring is compressed or elongated, the work done on the spring is stored as its potential energy.
A spring is elongated by a force F and the elongation is x, then F = kx [where k is the force constant] ——(1)
Now the spring is further stretched through a distance dx, therefore the work done for further stretching is
dw = F.dx = Fdx cos 00 = Fdx = kxdx [using equation (1)]
Therefore, the work done to stretch the spring through a distance x from its normal position(x = 0) is
W =
= 
kxdx =
kx2 = potential energy of spring.
Force constant calculation:
- Spring in series: Two massless springs of force constant k1 and k2 are connected in series as shown in figure. Due to applied force F on the body the body is displaced by x. As the springs are massless, so the force acts on each spring is also F. If x1 and x2 are the elongation of two springs of force constant k1 and k2 respectively, then F = k1x1 and F = k2x2. But x1 + x2 = x.
So, 
+ 
= x
If k is the equivalent force constant [replacing two springs by a single spring keeping force and elongation same] then, , + = 
. Therefore, in series connection of spring 
= 
+
.
- Spring in parallel: (i) Two massless springs of force constant k1 and k2 are connected in parallel as shown in figure. Due to applied force F, the body is displaced by x.
Therefore, the elongation of each spring is also x.
If F1 and F2 are the force applied on two springs of force constant k1 and k2 respectively,then F1 = k1x and F2 = k2x.
Here F = F1 + F2 = k1x + k2x = (k1 + k2)x
If k is the equivalent force constant [replacing two spring by a single spring keeping force and elongation same] then,
kx = (k1 + k2)x
Therefore, in parallel connection of spring k = k1 + k2.
(ii) In this figure when F force is applied on body towards right to displaced it by x, then spring k1 is expanded by x where F1 is the spring force produced. Similarly, spring k2 is compressed by x where F2 is the spring force. Therefore, F = F1 + F2 = k1x + k2x = (k1 + k2)x
If k is the equivalent force constant [replacing two spring by a single spring keeping force and elongation same] then, kx = (k1 + k2)x
Therefore, the equivalent force constant k = k1 + k2.
Concepts on spring problem:
- Two bodies of mass M and m (M>m) are placed on a smooth horizontal surface attached by a dynamometer. F and f (F>f) force are applied on M and m respectively as shown in figure. Find the reading of the dynamometer.
The acceleration of the system is a = 
.
If T is the reading of the dynamometer, then F – T = Ma
Or, T = F – M( ) = 
.
- F force is applied on mass M to displace it downwards by y. Find the value of F in terms of force constant k and displacement y.
In this figure, as the other end of the string is fixed, so the net displacement of the center of pulley is 
. Therefore, the elongation of spring is also .
For equilibrium of mass M, T = F
For equilibrium of pulley 2T = T/
For spring T/ = k
Or, 2T = k
F = k
.
- In this figure, when the mass M is displaced downwards by y, then the center of pulley also is displaced downwards by y. So, the elongation of spring is 2y [as the string is fixed, so the spring is elongated to provide sufficient length 2y].
For equilibrium of mass M, T = F
For equilibrium of pulley T = 2T/
For spring T/ = k2y
Or, T = k4y
F = 4ky.
Reaction of lift: A man of mass M is standing on a lift, where R is the reaction force acting on the man by lift.
- When the lift is stationary or moving with constant velocity: At this condition acceleration of the lift is 0. So, net force acting on man is R – Mg = 0 or, R = Mg.
- When the lift is moving with constant acceleration in upward direction: At this condition acceleration of the lift is a. So, net force acting on man is R – Mg = Ma
Or, R = Mg +Ma = M(g + a).
- When the lift is moving with constant acceleration in downward direction: At this condition acceleration of the lift is a. So net force acting on man is Mg – R = Ma
Or, R = Mg – Ma = M(g – a).
- When the lift is moving with acceleration g in downward direction: At this condition acceleration of the lift is g. So net force acting on man is Mg – R = Mg
Or, R = Mg – Mg = 0. This is known as weightlessness condition.
- When the lift is moving with acceleration greater than g in downward direction:
At this condition acceleration of the lift is a>g. After some time the ceiling of the lift touches the head of the man.
So, the reaction force acting on the man by lift is along downward.So, net force acting on man is
Mg + R = Ma or, R = Ma – Mg = M(a -g). This is known as super weightlessness condition.
Variable mass situation: According to Newton’s second law, = 
where F is the applied force and 
= m
is the momentum of the body. = 
= m 
+ 
. If is constant then = 0. So, = .
Friction: Friction is the retarding force which acts tangentially to the contact surface when a body actually moves or tends to move over the surface of another body.
Static friction: The force of friction which exactly counter-balance the applied force during the stationary state of a body is called static friction. So static friction is equal to the applied force. Static friction increases up to the maximum value (limiting friction) with increasing the applied force. So static friction is self-adjusted force.
Limiting friction: The maximum value of static friction which comes into play when a body is just going to start sliding over the surface of another body is called limiting friction.
Laws of friction: 1.The direction of limiting friction is always opposite to the direction in which motion takes place or tends to take place.
- The force of friction acts tangentially along the surface of contact of two bodies.
- The magnitude of frictional force (f) is directly proportional to the normal reaction (R) between the surfaces. f
R then f = µR where µ is the coefficient of friction.
4. Friction is independent of area of surface of contact of two bodies and depends on the nature of the surface.
Angle of friction: The angle between the normal reaction and the resultant of limiting friction and normal reaction is called angle of friction.
The resultant of limiting friction (f) and normal reaction (R) is represented by R’ = OC.
The angle θ between R and R’ is called angle of friction. So tanθ = 
but = µ. So, tanθ = µ.
The coefficient of friction is numerically equal to the tangent of the angle of friction.
Angle of repose: The minimum angle made by the inclined plane with the horizontal surface such that the body lying on the inclined plane is just at the verge of sliding down along the inclined plane is called angle of repose.
A body of mass m is placed on the inclined plane of inclination 
then the component of weight acting downward is F = mg sin and normal reaction force R = mgc0s . As the body remain at rest then, frictional force f = F = mg sin again f = µR where µ is the coefficient of friction.
So, µ = 
= 
= tan ——-(1)
If θ is the angle of friction, then, tan θ = µ —-(2)
From equations (1) and (2) we get, tan= tan θ so, = θ. Therefore, angle of friction = angle of repose.
Acceleration of a body on rough inclined plane: A body of mass m is placed on the inclined plane of inclination θ (θ > the angle of repose).The force acting downward along the inclined plane is
F/ = mgsin θ —-(1).
The frictional force fk acts upward along the inclined plane. fk = F = µkR where µk is the coefficient of kinetic friction.
The normal reaction force R = mgcos θ ——(2).
As the body moves downward along the inclined plane, then, ma = F/ – F = mgsin θ – µkmgcos θ .
Or, a = g( sin θ – µk cos θ )
Acceleration of a body on rough horizontal plane: A body of mass m is moving on rough horizontal plane due to force F. If fk is the frictional force then,
fk = µkR where R (= mg) is the normal reaction force. Then the acceleration of a body a = ( 
– µkg).
Friction related concepts:
1.A car of mass m is moving with speed u and brake is applied so that it travels distance s before stop. Find frictional force and coefficient of friction between the wheel and the road.
Using the equation v2 = u2 + 2as we get, 0 = u2 – 2as or, a = 
[retardation]
Therefore, frictional force F = ma = 
.
The normal reaction force N = mg.
Therefore, coefficient of friction between the wheel and the road is μ = 
=
= 
.
- A block of mass M is placed on smooth horizontal ground. Another block of mass m (< M) is places on M. The coefficient of static friction between M and m is μ . Now F force is applied on M. Find the value of F so that m tends to slide over M.
The acceleration of both the bodies remain same as m is not moving over M.
The acceleration is a = 
. The pseudo force experienced by m is ma = 
.
As m tends to slide over M, then ma = limiting friction.
Or, = μmg
F = μ (M+m)g.
- A particle of mass m is placed in the inner wall of a spherical shell of radius r. If coefficient of friction between the inner surface and the particle is μ=
, then at what height from the lowest point of the sphere the particle can be placed?
Let the particle can be placed at point A. The component of weight of the particle mgsin 
tend to move it downward. Therefore, friction (f) acts in the upward direction. For equilibrium of the particle, f = mgsin
Or, μN = mgsin
Or,μ mgcos = mgsin
Or, tan =μ =
∴ = 300
AC is perpendicular on OB. So, OC = OAcos = rcos = 
Height h = BC = OB – OC = r – = r(1 – 
).
- A block A of mass M is placed on horizontal table. Another block B of mass m is places on block A as shown in figure. Now F force is applied on B. The conditions are explained below.
(i) If there is no friction between A and B and between A and table, then B will move with acceleration aB = . There is no frictional force to move A on the table, so A remain rest.
If L is the length of A, then B takes t time to fall from A.
L = 
= 
∴ t = 
(ii) Friction presents in between A and B only and the coefficient of static friction between A and B is μ . The limiting friction between A and B is f = μmg. B will not slide on A till F < f i.e. F < μmg.
This f also acts on A by B. So, both will move with acceleration a = aA = aB = .
If F > f i.e. F > μmg , then A and B will move in same direction but with different acceleration. The net force on B is
F – f = (F – μmg ). The acceleration of B is aB = 
.
The net force on A is f = μmg . The acceleration of A is aA = 
.
(iii) Find the time when B falls from A: The acceleration of B with respect to A is
aBA = aB – aA = ( ) – ( ) = 
.
If L is the length of A, then B takes t time to fall from A, then, L =
∴ t = 
= 
.
If A remain rest on the table, then the friction between A and table is f not f/. [Because friction is a self-adjusted force and if the applied force is less than the limiting friction, then the value of static friction is equal to the applied force]
- A block A of mass M is placed on horizontal table. Another block B of mass m is places on block A as shown in figure. Now F force is applied on A. The conditions are explained below.
(i) If there is no friction between A and B and between A and table, then A will move with acceleration aA =
. There is no frictional force to move B on A, so B remain rest.
In this case B moves with acceleration aA with respect to A in the opposite direction of F.
If L is the length of A, then B takes t time to fall from A, then L =
= 
∴t = 
(ii) Friction presents in between A and B only then both will move with acceleration a = . The force on block B is F/ = ma =
. The coefficient of static friction between A and B is μ . The limiting friction between A and B is f= μmg. B will not slide on A till F/< f i.e. F/< μmg or, < μmg or, F < μg(M+m). Therefore, if F <μg (M+m), then both the bodies move with same acceleration aA = aB = .
If F >μg (M+m), then both the bodies move with different acceleration.
The net force on A is F – f = F -μmg . The acceleration of A is aA = 
.
The net force on B is f =μmg . The acceleration of B is aB =
= μg .
The acceleration of B with respect to A is aBA = aB – aA =µg – = – [
]
Negative sign indicates that B accelerates backward with respect to A. If L is the length of A, then B takes t time to fall from A.
L =
t = 
=
.
- Three blocks A, B and C each of mass m, 2m and 3m respectively are placed one over another as shown in figure. Block A is fixed with the wall by a massless rod. Block B and C are connected by inextensible string over a massless frictionless pulley. The coefficient of friction for all surfaces is µ. Find the force F applied on C to move it with constant speed.
The friction between block A and B is f1 = µmg.
Similarly the friction between block B and C is f2 =µ (m+2m)g = 3µ mg and fiction between block C and table is f3 = µ(m+2m+3m)g = 6µ mg.
As block C moves with constant speed towards left so Block B applies friction f2 on it towards right. Therefore, from free body diagram of C, F = f2 + f3 + T = 3µ mg + 6µ mg + T = 9µ mg + T —— (i)
Block C applies frictional force on B towards left. As A is rest and B moves towards right then A applies frictional force on B towards left.
Therefore, from free body diagram of B, T = f1 + f2 = µmg + 3 µmg = 4µ mg ——-(ii)
From equation (i) and (ii) we get, F = 9µ mg + 4µ mg = 13µ mg.
- A rod of length l weight w rests with end A on rough vertical wall and end B is on rough horizontal surface. The coefficient of friction between rod and wall is
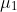and coefficient of friction between rod and ground is 
. If the rod is in equilibrium, then find the minimum value of for which the rod tends to slide on ground.
Let us consider the reaction forces act on the rod at point A and B are R1 and R2 respectively. The frictional force act at point A and B is f1 = R1 and f2 = R2 respectively.
As the rod is in equilibrium then, R1 = f2 = R2 [
= 0 ——- (i)
And f1 + R2 = w or, R1 + R2 = w [
=0 ——- (ii)
For the rotational equilibrium of the rod, torque is zero. So, taking toque about point B we get,
– R1.BC – f1.BO + w.BE = 0
Or, w.BDcos = R1BAsin + f1BAcos
Or, wlcos = R12lsin + f12lcos
Or, 2R1sin = cos (w – 2f1)
Or, tan = 
Or, tan = 
[using equation (ii)]
Or, tan =
Or, tan = 
[using equation (i)]
Or, tan = 
∴ = 
()
9. The length and mass of a chain is L and M respectively. If 
part of the chain is hanged from a rough table then the remaining part tends to side from the table. If the chain is released when half part is hanging from the table, then calculate the speed of the end of the chain during leaves the table.
If the coefficient of friction between the table and chain is μ, then friction between the table and chain = weight of the hanging part
Or,
= 
∴μ = 
.
Let us consider x (> part of the chain) is the length hanging from table. Then force acting on the chain is
F = 
– 
= 
– 
= 
= 
Acceleration of the chain a = 
= 
= 
– 
v
= 
– 
Or, vdv = (– )dx
Or, 
vdv = 
(
– )dx
or, 
= 
or, = 
– 
or, = 
–
or, = 
∴v = 
Application of force on inertial and non-inertial frame of reference:
Let us consider a lift is moving downward with an acceleration and a block of weight w is on the floor of the lift. An observer A is inside the lift and another observer B is standing on ground. The force of reaction R applied on block by the floor vertically upward. The net force acting on the block is (w-R) vertically downward.
We now consider a frame of reference attached to the lift. For the observer A, who is at rest in this reference frame observes the block is at rest. I.e. its acceleration is zero. So, from Newton’s first law, he concludes that no net force acts on the block, i.e. w – R = 0 or, w = R.
Now in the reference frame fixed on the earth, the observe B is at rest. He observes that the block is falling vertically downward with the lift with acceleration a. So, from Newton’s first law he concludes that a net force is acting on the block, i.e. w – R ≠ 0 or, w ≠ R.
So, two observers reach different conclusions regarding the forces applied on the block.
Inertial frame of reference: A frame of reference in which Newton’s first law holds good is called an inertial frame of reference. All frames which are at rest or moving with uniform speed relative to an inertial frame are also inertial.
Non-inertial frame of reference: A frame of reference in which Newton’s first law does not hold good is called non-inertial frame.
Let us consider, a frame X is moving with acceleration A with respect to an inertial frame Y.
The acceleration of particle on frame Y and X are a and , then a = a/ + A. If m is the mass of the particle, then ma = ma/ + mA. As Y frame is inertial, then Newton’s law is valid on it and F = ma.
So, a/ = 
. Therefore F ≠ ma/ and Newton’s law is not valid on frame X. Therefore, all the frames which are accelerating with respect to an inertial frame is non-inertial.
From equation ma/ = ma – mA = F – mA where –mA is the pseudo force.
.
Pseudo force: A force that appears on observer only due to acceleration of a frame of reference and acts in a direction opposite to that of the frame of reference is called pseudo force.
When a vehicle accelerates, a passenger leans backwards. As the vehicle’s acceleration is in the forward direction, so a pseudo force acts on the passenger in the backward direction.
Concepts on inertial and noninertial frame of reference:
1.A pendulum is hanging from the roof of a car which moves in the horizontal direction with acceleration a. If the string remains inclined at an angle with the vertical, then determine the tension on the string. Mass of the bob of the pendulum is m.
As the car is moving with an acceleration a in the horizontal direction towards right, so the bob of the pendulum experience a pseudo force ma in opposite direction (horizontally towards left). If T s the tension on the string then Tcos = mg and Tsin = ma
∴ T = 
= m
.
- A block of mass m is placed on a wedge of mass M as shown in figure. All the surfaces are frictionless. Find the force F is applied on wedge so that the block remains stationary with respect to wedge.
As the block is stationary with respect to wedge and wedge is on a frictionless surface, then both are moving with same acceleration a = .
Observe from ground (inertial frame of reference): From free body diagram of the block we get, R is the normal reaction applied on block by wedge. With respect to ground the block is moving with acceleration a. Therefore, after perpendicular resolution of R we get, Rcos = mg —– (i) [
= 0
AndRsin = ma ——- (ii) [
= ma
From equation (i) and (ii) we get, tan = 
=
Therefore, F = (M+m)gtan .
Observe from wedge (noninertial frame of reference): With respect to wedge the block is stationary and it is placed in a accelerated frame, therefore pseudo force ma acts on it. From free body diagram of the block we get, R is the normal reaction applied on block by wedge.
Therefore, after perpendicular resolution of R we get, Rcos = mg —– (i) [ = 0
AndRsin = ma ——- (ii) [ = 0
From equation (i) and (ii) we get, tan = =
Therefore, F = (M+m)gtan .
- A block of mass M is connected with a wedge of mass M/ by a massless inextensible string over a massless frictionless pulley. Another block of mass m is placed on the wedge. Find the mass M of the hanging block for which m remain stationary on the wedge. All the surfaces are frictionless.
Let us consider R is the normal reaction between wedge and block m.
The downward acceleration of block of mass M is a.
Using free body diagram of block of mass M we get, Mg – T = Ma
Or, T = Mg – Ma —- (i)
Using free body diagram of wedge we get, T – Rsin = M/a —- (ii)
Using free body diagram of block of mass m we get, Rcos = mg —— (iii)
Rsin = ma —- (iv) [ma is the pseudo force experienced by m]
From equation (iii) and (iv) we get, tan = —– (v)
From equation (ii) and (iv) we get, T – ma = M/a —- (vi)
From equation (i) and (vi) we get, Mg – Ma = ma + M/a
Or, a = 
—— (vii)
From equation (v) and (vii) we get, gtan =
∴ M = 
.
- The coefficient of friction between a wedge of mass M and a block of mass m is . Find the minimum horizontal force F is required to keep the block stationary with respect to the wedge.
As the block remain stationary with respect to the wedge, then the acceleration of the system is a = .
Observing from inertial frame of reference: If the block is observed from ground, only real force is acting on it. With respect to ground the block is moving with acceleration a and the reaction force acting on block by wedge is N.
Therefore, N = ma —— (i)
As the block remain stationary with respect to the wedge, so frictional force f = mg or,μ N = mg —– (ii)
From equation (i) and (ii) we get, μma = mg or, a = 
.
Therefore, force F = (M + m)a =
.
Observing from noninertial frame of reference: If the block is observed from wedge, then real and pseudo forces are acting on it. With respect to wedge the block is stationary so, pseudo forces FP = ma acting on it in the direction of opposite to the acceleration of wedge. The reaction force acting on block by wedge is N.
Therefore, N = FP = ma —— (i)
As the block is not moving downward with respect to the wedge, so frictional force f = mg or,μ N = mg —– (ii)
From equation (i) and (ii) we get, μma = mg or, a = .
Therefore, force F = (M + m)a = .
5. A block of mass m is placed on an inclined surface of a wedge of mass M. If all the surfaces are frictionless then calculate the acceleration of block and the wedge when the block is released.
Let us consider N is the normal reaction force between the block and the wedge. Due to N, wedge moves towards left with acceleration a.
Using free body diagram for wedge we get, Nsin = Ma —— (i)
As the block moves on the inclined surface of the wedge, there are vertical and horizontal force acting on block with respect to ground. Let us consider acceleration of block on the inclined surface in downward is b.
Using free body diagram for block we get, mg – Ncos = mbsin —– (ii)
Nsin + ma= mbcos ——- (iii) [as the wedge is accelerating then block will experiences a pseudo force ma]
From equation (i) and (iii) we get, Ma + ma = mbcos
Or, a = 
——- (iv)
From equation (i) and (ii) we get, mg – 
= mbsin
Or, m(g – bsin ) = Macot
Or, a = 
——- (v)
From equation (iv) and (v) we get, =
Or, Mbcos cot = (M + m)g – (M + m) bsin
Or, b[ 
+ (M + m)sin ] = (M + m)g
Or, b[M( 
+ 
) + m ] = (M + m)g sin
∴ b =
Therefore, a = (
){ } = 
.
Two bodies of mass m and M (M>m) are connected by inextensible massless string over a massless frictionless pulley. The pulley is hanged from the ceiling of a lift which is moving upward with acceleration a. Find the acceleration of the bodies with respect to lift.
Observing from inertial frame of reference (ground): Let us consider the acceleration of the bodies with respect to pulley is a0.
Acceleration of body of mass m with respect to pulley = acceleration of body of mass m with respect to ground – acceleration of pulley with respect to ground.
Or, a0 = a1 – a or, a1 = a0 + a
Similarly, acceleration of body of mass M with respect to pulley = acceleration of body of mass M with respect to ground – acceleration of pulley with respect to ground.
Or, – a0 = a2 – a or, a2 = – a0 + a
If T is the tension on the string then, T – mg = ma1 or, T – mg = m(a0 + a) —— (i) [using free body diagram of m]
And T – Mg = Ma2 or, T – Mg = M( – a0 + a) —— (ii) [using free body diagram of M]
From equation (i) and (ii) we get, mg + m(a0 + a) = Mg + M( – a0 + a)
Or, Mg + Ma – mg – ma = ma0 + Ma0
Or, a0 = 
.
Observing from noninertial frame of reference (lift): Let us consider the acceleration of the body of mass m with respect to pulley is a0 in upward direction and for mass M it is a0 in downward direction.
As the lift is moving upward with acceleration a, then two bodies will experience pseudo force.
If T is the tension on the string then, T – mg – ma = ma0 —— (i) [using free body diagram of m]
And Mg + Ma – T = Ma0 —— (ii) [using free body diagram of M]
From equation (i) and (ii) we get, Mg + Ma – mg – ma – ma0 = Ma0
Or, Mg + Ma – mg – ma = ma0 + Ma0
Or, a0 = .
Centripetal and centrifugal force: When the motion of a body is observed from a rotating reference frame, a pseudo force called centrifugal force comes into play. Where centripetal force is a real force which acts from body to centre of rotation. Centrifugal force acts from the centre of rotation to the body. Both the centripetal force and centrifugal force have same magnitude 
. Where a body of mass m rotates in a circular path of radius r with speed v.
tag:
Share:
koushiadmin
