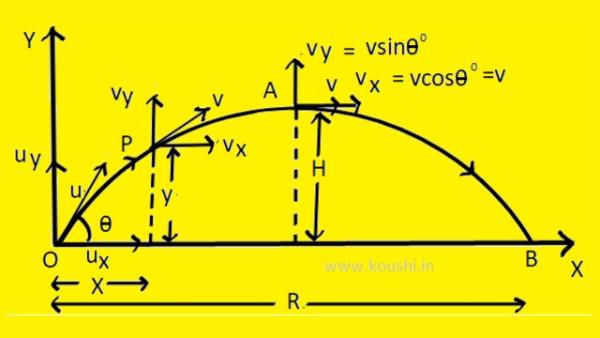
Velocity: Let us consider vx and vy are the horizontal and vertical component of velocities at point P(x, y). As gravitational acceleration (g) acts downwards, then horizontal component of acceleration is gcos900 = 0.
So, vx = ux = ucos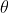 ——–(1)
——–(1)
And vy = uy – gt = usin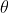 – gt ——–(2)
– gt ——–(2)
So, the magnitude of velocity of particle at point P is v = 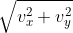 ——–(3)
——–(3)
Displacement: Let us consider, the coordinates of point P is (x, y).
So, x = uxt = utcos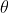 ——–(4)
——–(4)
And y = uyt –  gt2 = utsin
gt2 = utsin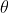 –
–  gt2 ——-(5)
gt2 ——-(5)
The trajectory of the motion is y = usin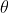 (
(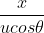 ) –
) –  g(
g(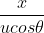 )2
)2
y = xtan –
–  g(
g(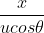 )2 ——–(6) This is the equation of parabola.
)2 ——–(6) This is the equation of parabola.
Maximum height: At point A, particle is at maximum height. At point A, the velocity of the particle is along the tangent. So, vy= 0.
Therefore, usin – gt = 0 [using equation (2)]
– gt = 0 [using equation (2)]
∴ t = 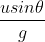
Substituting the value of t in equation (5) we get, maximum height
H = usin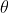 (
(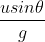 ) –
) –  g(
g(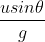 )2
)2
∴ H = 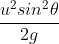 ——— (7)
——— (7)
Time of flight: The total time taken by the particle during its motion is T. During time of flight then the net displacement along y axis is 0. From equation(5) we get, uTsin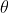 –
–  gT2 = 0
gT2 = 0
∴T = 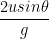 ——–(8)
——–(8)
Range: The maximum horizontal distance travelled by the body is called range.
Range R = uxT = ucos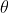 (
(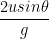 ) =
) = 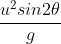 .
.