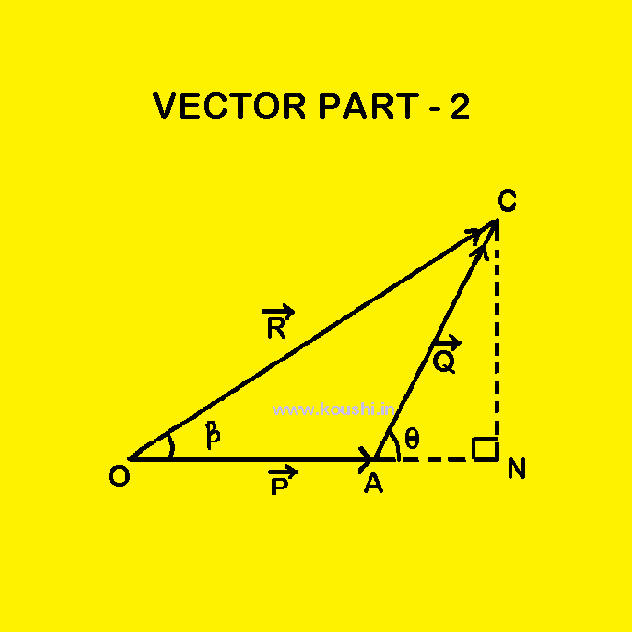
Triangle law of vector addition:
Statement: If two vectors are represented both in magnitude and direction by two sides of a triangle taken in the same order, then the resultant of these vectors is represented both in magnitude and direction by the third side of the triangle taken in the opposite order.
Prove: Let us consider 
 and 
 acting simultaneously on a particle be represented both in magnitude and direction by two sides OA and AC of 
OAC taken in the same order. 
 is the resultant of  and is represented by side OC. So,  = +
CN is the perpendicular on ON and θ is the angle between  and .
In right-angled ONC, OC2 = ON2 +NC2
Or, R2 = (OA + AN)2 + NC2Â
Or, R2 = OA2 + AN2 + 2OA.AN + NC2Â
Or, R2 = OA2 + AN2 + 2OA.ACcos
+ NC2
 R2 = OA2 + AC2 + 2OA.ACcos
[From right-angled ANC, 
 = 
 so, AN = AC  and AN2+ NC2 = AC2]
R2 = P2 + Q2 + 2PQ
Let us consider 
creates angle 
 with 
. Then from right-angled ONC, 
 = 
= 
= 
Or, = 
[From right-angled ANC, 
 = 
].
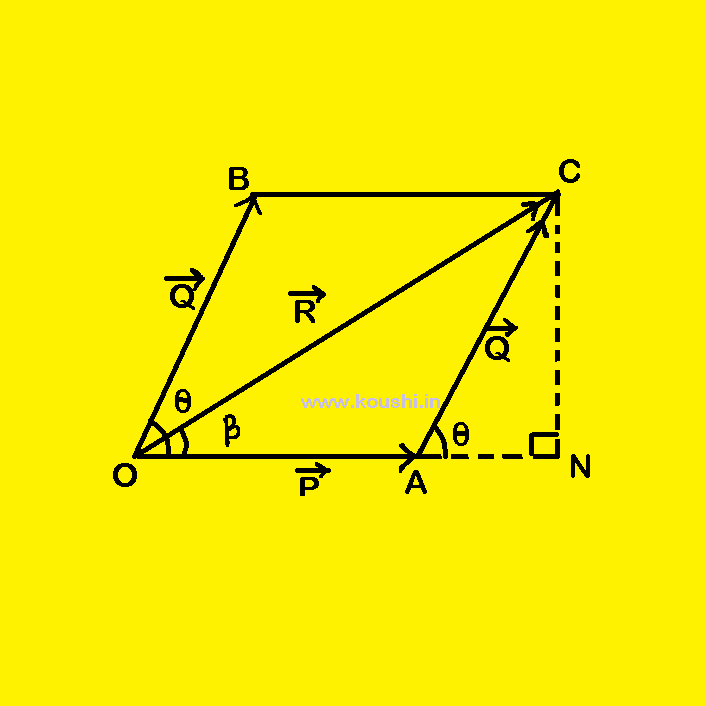
Parallelogram law of vector addition:
Statement: If two vectors are represented both in magnitude and direction by two adjacent sides of a parallelogram drawn from a point, then their resultant will be represented both in magnitude and direction by the diagonal of the parallelogram drawn from that point.
Prove: Same as triangle law.
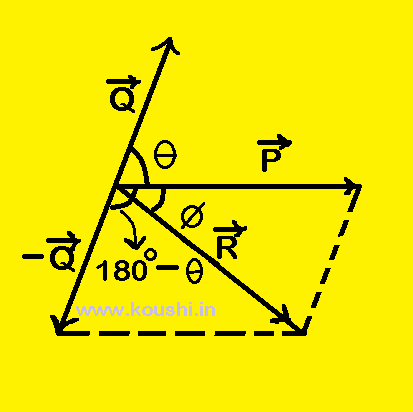
Subtraction of vectors:
Let us consider  and  creates angle θ. To subtract  from  we can write + (- ) [where –  is the opposite vector of ]. The angle between  and –  is (180 – θ) and  is the resultant of  and – .
The magnitudes of  is R2 = P2 + Q2+2P.Q
Â
Or, R2 = P2 +Q2– 2PQÂ
If creates angle 
 with then tan = 
 tan = 
.
