Class - XI Free Courses
...
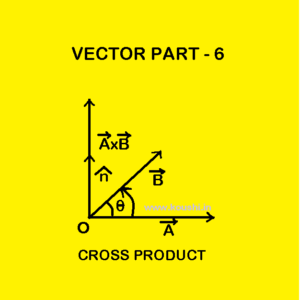
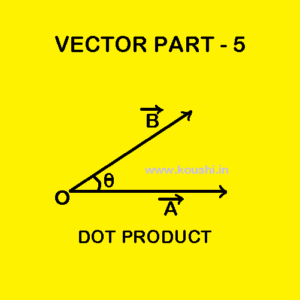
Vector For Class - XI
We Provide free courses for Class XI
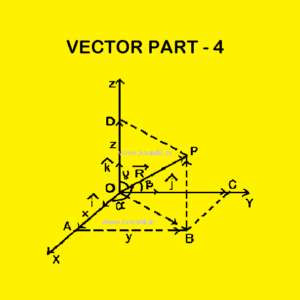
Vector Part 4
Representation of a vector by coordinates: Let us consider OX,...
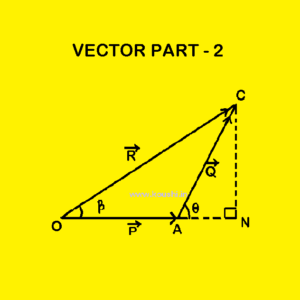
Read MoreVector Part 2
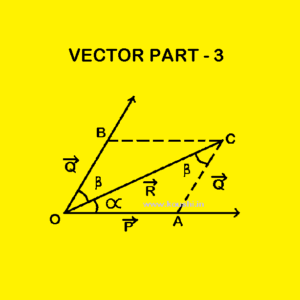
Triangle law of vector addition: Statement: If two vectors are...
Read MoreVector Part 1
Scalar: The quantities which are represented by magnitude and no...
Read More