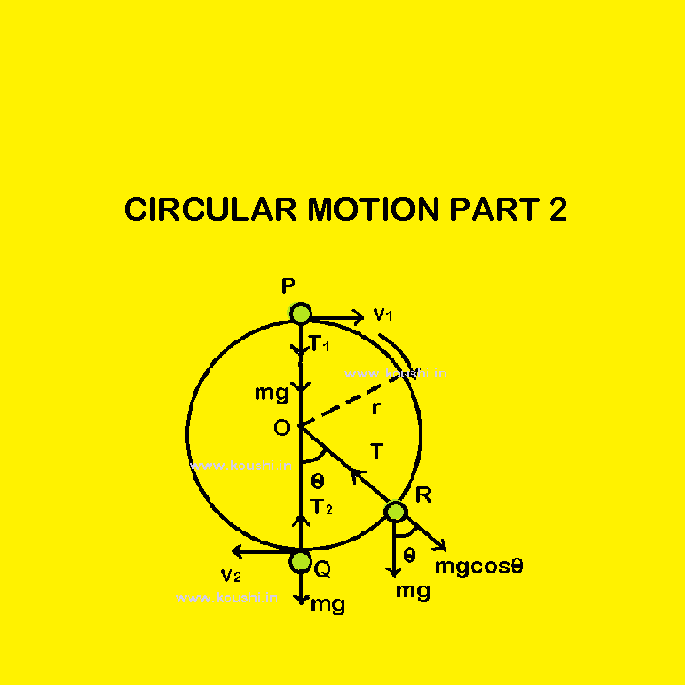
Circular motion of a body in vertical plane: A body of mass m is moving in a circular path of radius r in a vertical plane using an inextensible massless string. The velocity of the body at highest point (point P) is v1 and velocity at lowest point (point Q) of its motion is v2. The tension of the string at point P and Q are T1 and T2 respectively.
The force acting on the body at point P towards the centre of the circle is
mg + T1 = 
(centripetal force). But at point P, T1 = 0. So, v1 = 
——(1)
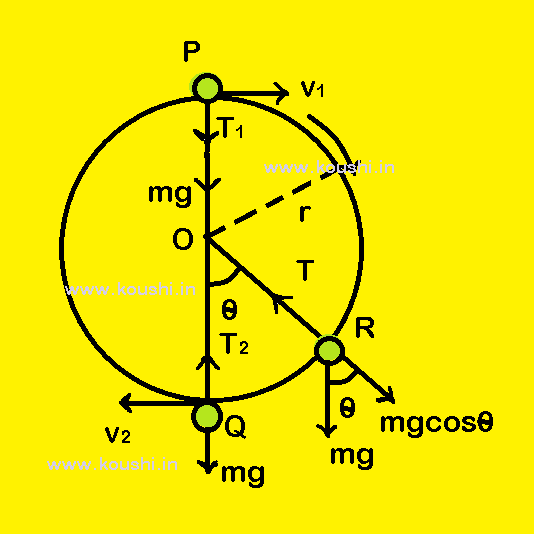
At point Q the force towards the centre of the circle is T2 – mg = 
(centripetal force) ——(2)
The energy at point P is EP = mg2r + 
and the energy at point Q is EQ = 
. As the energy is conserved, then EP = EQ.
So, mg2r + =
Or, 4gr + v12 = v22
Or, 4gr + gr = v22 [using equation (1)]
v2 = 
——(3)
From equation (2) and (3), we get, T2 – mg = 5mg
T2 = 6mg.
So, the tension on the string at the lowest point is 6 time the weight of the body.
When the body is at point R, the speed of the body is v and tension of string is T, then 
= T – mgcos
.
So, T = + mgcos.
The energy at point R is ER = 
.
Using conservation of energy at point P and R we get, = mg(r + rcos) +
Or, 
= 2gr(1 + cos) + rg = rg(3 + 2cos)
v = 
.
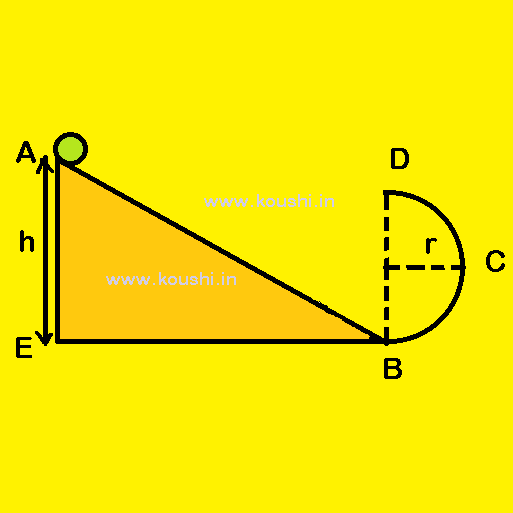
Concept on vertical circular motion: A ball is released from the top of an inclined plane. The lower part of the inclined plane is connected with a vertical circular path of radius r. Find the minimum height from which the ball is released so that it can move through the circular path. [Consider all the surfaces are frictionless]
To move through the circular path, the required velocity at point B is v = .
Using conservational of mechanical energy at point A and B we get, potential energy at point A = kinetic energy at point B
Or, mgh =
h = 
= 2.5r.
