The basic information of angular displacement, angular velocity and angular acceleration is given in Free Course-Class IX-Motion. To get this click the button.
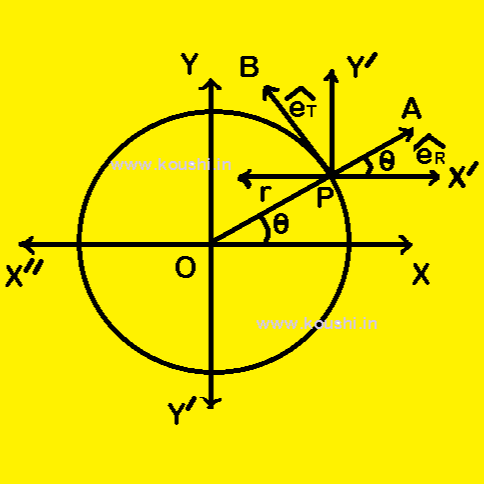
Unit vectors along the radius and tangent: Let us consider OX and OY are two mutual perpendicular axes and O is the origin. A particle is moving in a circular path of radius r. At any instant the particle is at point P in the circle and angular position of the particle at this instant is 
.
Let us consider 
 = 
 along the outward radius and 
 = 
 along the tangent in the direction of increasing . 
 is the radial unit vector and 
the tangential unit vector. Draw 
parallel to the X-axis and 
parallel to the Y-axis.
From the figure, = PAcos
+ PAsin
 or,  = 
 = cos + sin ———–(i)
Where and are the unit vectors along the X and Y axes respectively. Similarly, = – PBsin + PBcos
Or, Â = 
= – sin + cos ———–(ii)
Velocity of the particle in circular motion: Let us consider OX and OY are two mutual perpendicular axes and O is the origin. A particle is moving in a circular path of radius r. At any instant the particle is at point P in the circle and angular position of the particle at this instant is .  = cos + sin is the radial unit vector and  = -sin + cos is the tangential unit vector. The position vector of the particle at time t is 
 = 
 = OPcos + OPsin = r(cos + sin) ……..(i)
Differentiating equation (i) with respect to time, the velocity of the particle at time t is 
= 
= 
[r(cos + sin)]
= r [- sin
+ cos]
= rω[- sin + cos] Â
= rω ……..(ii) [where ω =  and = – sin + cos]
The term rω is the speed of the particle at time t and the velocity vector is directed along the tangent. Thus, the velocity of the particle at any instant in circular motion is along the tangent to the circle and its magnitude is v = rω.
Acceleration of the particle in circular motion: Differentiating equation (ii) with respect to time, the acceleration of the particle at time t is
 = 
 = r[ω (- sin + cos) + 
(- sin + cos)] Â
= rω[- cos + (-sin)] + r
= – ω2r[cos + sin] + r
= – ω2r + 
 ———-(iii) [where r = 
 = ].
Nonuniform circular motion: If the speed of the particle moving in a circle is not constant, the acceleration has both the radial and the tangential components. From equation (iii), the radial component of acceleration (towards the centre) is 
 = ω2r = 
 and the tangential component of acceleration is 
 = .
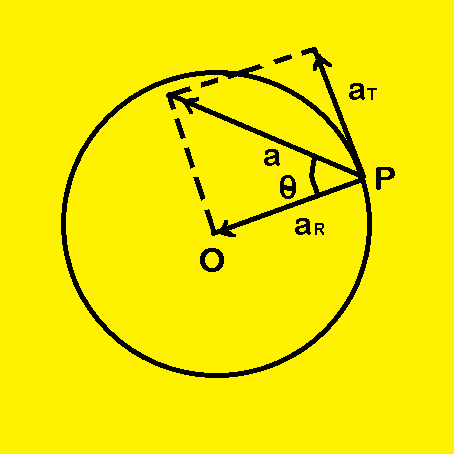
The magnitude of the acceleration is a = 
 = 
 ——–(iv)
Â
The direction of this resultant acceleration makes an angle  with the radius where tan = 
 = 
 ——–(v)
Example: A particle moves in a circle of radius 8 m. Its linear speed is given by v = t2, where t is in second and v in ms-1. Find the acceleration at t = 4 s.
The tangential acceleration is aT = Â = 
 = 2t = 2
4Â = 8 ms-2
The linear speed at t = 4 s is v = 
 = 16 ms-1
The radial acceleration at t = 4 s is aR = Â = 
 = 32 ms-2
Therefore net acceleration of the particle a = Â = 
 = 32.98 ms-2.
Directed at an angle = 
= 
 with radius at 4 s.
Uniform circular motion:  If the particle moves in the circle with a uniform speed v, then it is in uniform circular motion. In this case, = 0 and from equation (iii) we get = – ω2r  Thus, the acceleration of the particle is directed towards the centre. The magnitude of the acceleration is = ω2r =(
)r = .
This acceleration is called centripetal acceleration. The speed remains constant. The direction of motion of particle continuously changes and hence the velocity changes and there is an acceleration during the motion.
Example: Find the magnitude of the linear acceleration of a particle moving in a circle of radius 2 m with uniform speed completing the circle in 4 s.
The distance covered in completing the circle is 2Ï€r = 2Ï€2 m. The linear speed is v = 
 = 
 = π ms-1
The linear acceleration is a = Â = 
 = 4.9 ms-2
This acceleration is directed towards the centre of the circle.
Click the button to get the video explanation of ths part.