Reflection through curved surface Part – 1
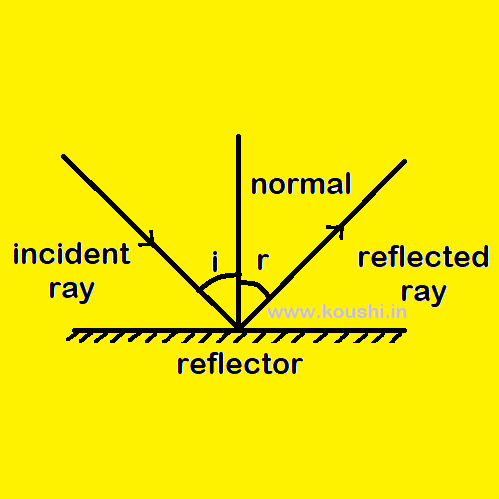
Laws of reflection: 1st Law -The incident ray, the reflected ray, and the normal, all lie on the same plane, called the plane of incidence. The incident and reflected rays are on the opposite side of the normal.
2nd Law – The angle of incident is always equal to the angle of reflection.
If 
i and r are the angle of incidence and angle of reflection then, i = r.
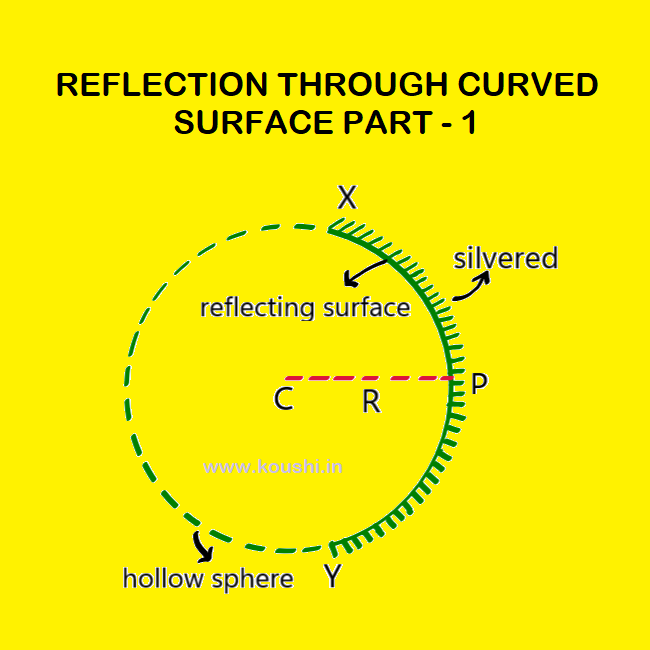
Reflection through spherical surface:
Centre of curvature: The centre of a hollow sphere of which the curved spherical mirror forms a part is called centre of curvature. It is denoted by C.
Radius of curvature: The radius of a hollow sphere of which the curved spherical mirror forms a part is called radius of curvature. It is denoted by R = PC.
Pole: The middle point of a spherical mirror is called pole. It is denoted by P.
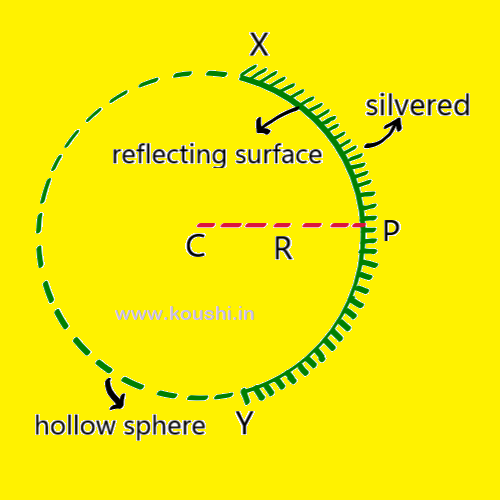
Aperture: The part of a spherical mirror exposed to the incident light is called the aperture of the spherical mirror. It is the diameter of the spherical mirror. It is denoted by XY.
Principle axis: A line joining the centre of curvature (C) and pole (P) of a spherical mirror is called principle axis.
Principle focus: A point on the principle axis of the spherical mirror where all the rays of light parallel to the principle axis meet or appear to meet after reflection from the spherical mirror is called principle focus. It is denoted by F.
Focal plane: A plane normal to the principle axis and passing through the principle focus (F) of a spherical mirror is called the focal plane.
Focal length: The distance between the pole (P) and the principle focus (F) of a spherical mirror is called focal length of the mirror. It is denoted by f (PF).
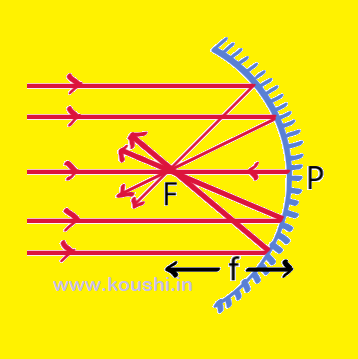
Sign convention for reflection by spherical mirror:
1. All the distances are measured from the pole of the spherical mirror.
2. Distances are measured in the direction of incident ray are taken as positive, and the distances are measured in the opposite direction of incident ray are taken as negative.
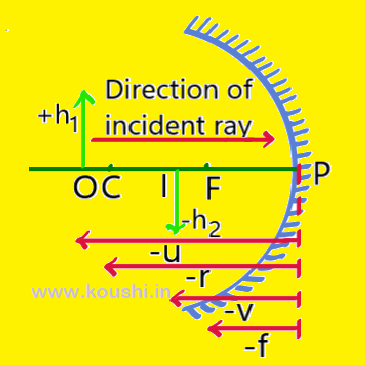
3. The upward distances (erect) perpendicular to the principle axis are taken as positive and the downward distances (inverted) perpendicular to the principle axis are taken as negative.
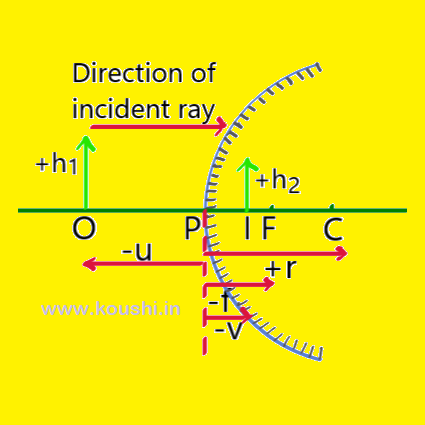
Relation between focal length and radius of curvature:
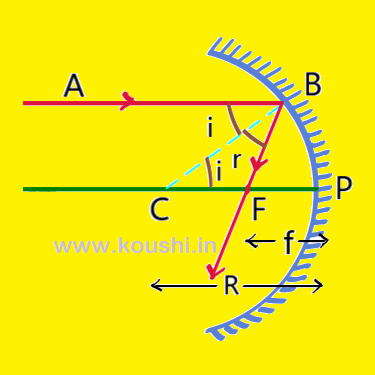
Let us consider AB is the incident ray parallel to the principle axis of a concave mirror of radius of curvature R (= PC) and focal length f (= PF). After reflection from point B the ray pass through the focus F. CB is the normal at point B. 
is the angle of incidence and 
is the angle of reflection.
[i.e. i = r] ——-(1)
[alternate angle] ——(2)
So, from equation (1) and equation (2) so, FC = FB ——-(3).
Since point B is very closed to P and the aperture of the mirror is very small, so instead of B we can write P. i.e. FB = PF ——(4).
From equation (3) and equation (4) FC = PF,
Or, PF = PC – FC
Or, PF = PC – PF
Or, 2PF = PC
Or, 2(-f) = (-R)
f 
.
Click the button to go to the next part of this chapter.
tag:
Share:
Admin Koushi
2 Comments
I found this article really informative and engaging. The site is always a reliable source
of knowledge.
Thanks for visit my site.