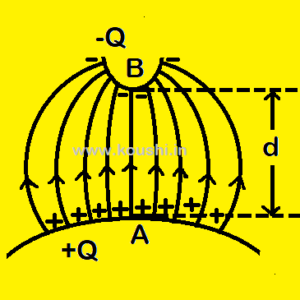
Capacitance due to variable electric field: If the two conductors A and B carry equal and opposite charges create a non-uniform electric field then find the capacitance of the system. The distance between the conductors is d.
If Q is the charge of each conductor and electric field E = 
(a + by) varies along y axis [where a, b and K are constant] then potential difference between the conductors is dV = – Edy = – (a + by)dy.
Net potential difference between the conductors
A and B is 
= – 
(a + by)dy
Or, V = VA – VB = [ad + 
]
So, capacitance C = 
 = 
.
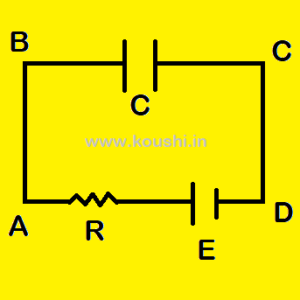
Function of resistor in the circuit of capacitor:
The function of capacitor is to store the charge and resistance is used to limit the current in the circuit during charging and protect the capacitor and battery from damage. So, in steady state there is no close path for current so the resistances are ineffective. Therefore, the potential difference against the capacitor is VB – VC = E.
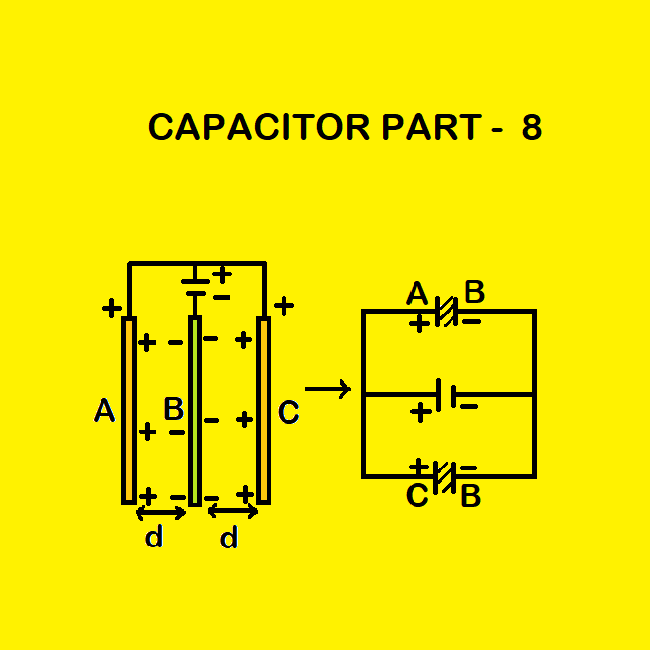
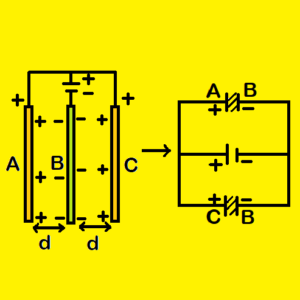
Three plates (A, B and C) each of plate area A are separated by distance d. The positive terminal of a battery is connected with plate A and plate C and the negative terminal is connected with plate B. What is the capacitance of the system?
The inner face of plate A and left face of plate B forms a parallel plate capacitor of capacitance C1 = 
. Similarly, the inner face of plate C and right face of plate B also forms a parallel plate capacitor of capacitance C2 = . Capacitors C1 and C2 are connected in parallel. So, the equivalent capacitor is C = C1 + C2 = 
.
Calculate the capacitance of the system where all the plates of equal area A and separated by distance d.
At first write the potential of each plate and then arrange the plates with respect to their potentials. As plate 3 is connected with positive terminal of a battery of emf V, its potential is V and the potential of plate 5 is 0.
Let us consider the potential of plate 1 and 4 is V1 as they are connected by a wire and the potential of plate 2 is V2.
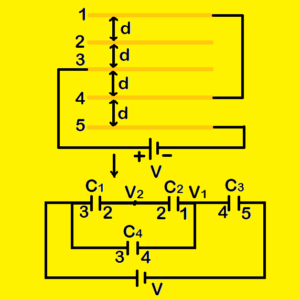
Now upper surface of plate 3 (potential is V) and lower surface of plate 2 (potential V2) form a capacitor C1. The upper surface of plate 2 and lower surface of plate 1 (potential V1) form a capacitor C2 which is in series connection with C1. Similarly, the lower surface of plate 4 (potential V1) and upper surface of plate 5 (potential 0) form a capacitor C3 which is in series connection with C2. The lower surface of plate 3 (potential V) and upper surface of plate 4 (potential V1) form a capacitor C4 which is in parallel connection with the series combination C1 and C2.
Here all capacitors have same capacitance C = .
So, the equivalent capacitance of C1 and C2 is 
 and equivalent capacitance of C1
and C2 and C3 is  + C = 
. The net capacitance of the combination is 
 = 
.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.