Kirchhoff’s law for capacitor:
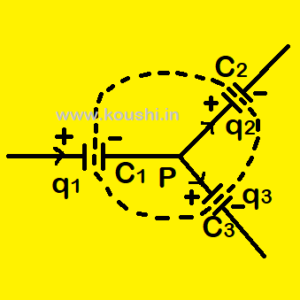
(i) Junction law: It states that in any isolated system of capacitor the net charge is conserved. So, the incoming charge at any junction is equal to the outgoing charge from the junction.
At point P the charge incoming is taken as positive and charge outgoing is taken as negative. So, q1 – q2 – q3 = 0.
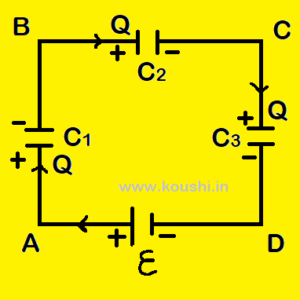
(ii) Loop law: The algebraic sum of voltage drop in a closed circuit of capacitor is zero. For the close loop ABCDA we get, VA – VB = 
VB – VC = 
VC – VD = 
So, VA – VD =  +  +  —— (i)
Again VA – VD = 
 ——- (ii) where  is the emf of cell.
Â
From equation (i) and equation (ii) we get  =  +  +  or,  +  +  –  = 0.
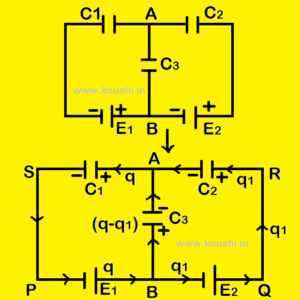
Example: Find the potential difference between the points A and B using Kirchhoff’s rule.Â
Let us consider q charge is entering at point B where q1 charge passes through E2 and (q – q1) charge passes through C3. Using KVL for the loop PBASP we get, (VP – VB) + (VB – VA) + (VA – VS) + (VS – VP) = 0
Or, – E1 + 
 + 
 + 0 = 0
Or, qC1 – q1C1 + qC3 = E1C1C3
Or, q(C1 + C3) – q1C1 = E1C1C3 ——-(i)
Using KVL for the loop BQRAB we get (VB – VQ) + (VQ – VR) + (VR – VA) + (VA – VB) = 0
Or, – E2 + 0 + 
 –  = 0
Or, qC1 – q1C1 + qC3 = E1C1C3
Or, q(C1 + C3) – q1C1 = E1C1C3 ——-(i)
Using KVL for the loop BQRAB we get (VB – VQ) + (VQ – VR) + (VR – VA) + (VA – VB) = 0
Or, – E2 + 0 + Â – Â = 0
Or, q1C3 – qC2 + q1C2 = E2C2C3
Or, – qC2 + q1(C2 + C3) = E2C2C3 ——-(ii)
Subtracting equation (i) from equation (ii) we get, q(C1 + C2 + C3) – q1(C1 + C2 + C3) = E1C1C3 – E2C2C3
Or, q – q1 = 
.
Therefore VA – VB = –  = 
.
Nodal analysis of capacitive circuit:
(i) At first identify different nodes and write their potential in the circuit.
(ii) Identify the isolated systems in the capacitive circuit and make equations using conservation of charge.
(iii) Solve the equations to get the values of potential at different points.
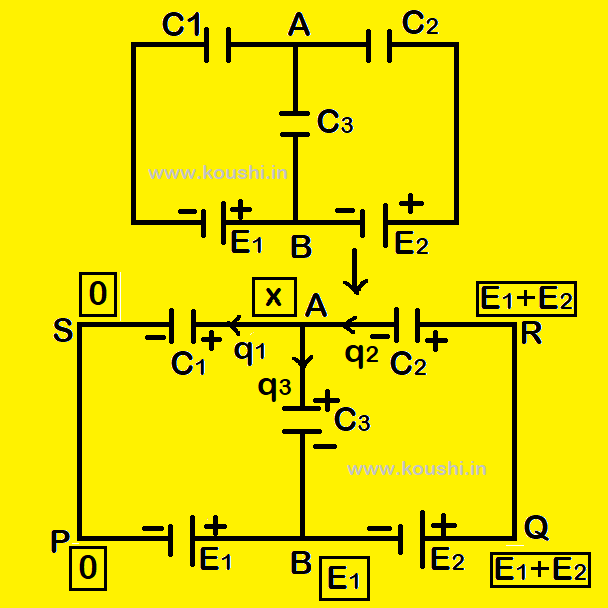
Find the potential difference between the points A and B using this concept:
Let us consider the potential at point B is E1 so potential at point P and S are 0. The potential at point Q is (E1 + E2).
Let the potential at point A is x so potential at point R is (E1 + E2).
Now consider the isolating system and taking charge entering the point A is equal the charge leaving point A.
So q1 + q3 = q2 or, C1x + C3(x – E1) = C2(E1 + E2 – x)
Or, C1x + C3x – C3E1 = C2E1 + C2E2 – C2x
Or, x = 
So, the potential difference between the points A and B is
VA – VB = x – E1 =  – E1 = 
.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.