Capacitance:
If the charge of a conductor is increased then the potential of the conductor is also increased.
Thus, charge (Q) 
potential (V) or, Q = CV ——–(1) where C is the capacitance of the conductor and that conductor is called capacitor.
From equation (1) C = 
——-(2) so, the capacitance of the conductor is thus defined as the amount of the charge stored per unit potential difference.
From equation (2), if v = 1 then Q = C. So, the capacitance of the conductor is thus numerically equal to the amount of charge required to increase its unit potential difference.
1 farad (F) = 
and 1stat farad = 
.
1 farad (F) = 
= 9 
1011 stat farad.
Capacitance of an isolate spherical conductor:
Let us consider a spherical conductor of charge Q and radius r is placed in air (dielectric constant of air is 1).
In C.G.S. system the potential of the conductor is V = 
.
If C is the capacitance of the conductor, then C = = R.
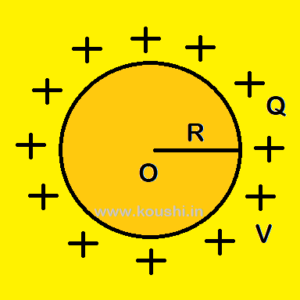
So, the capacitance of the spherical conductor is numerically equal to the radius of that conductor in C.G.S. system.
Principle of capacitor: A capacitor consists of two conductors separated by dielectric medium. One of the conductors is charged, whereas the other is earthed. The capacitance of charged conductor is increased by placing it near an earth-connected uncharged conductor.
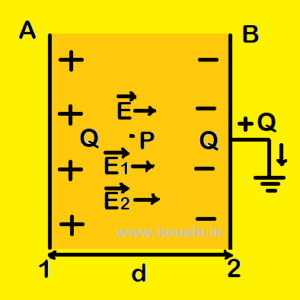
Capacitance of a parallel plate capacitor (without dielectric): Let us consider a parallel plate capacitor consists of two parallel plates (A and B) each of plate area A and the separation between the plates is d.
A plate is charged by Q and the outer surface of B is earthed. So –Q charge is induced in the inner surface of B. If σ is the surface charge density of each plate then the electric field between the plates is 
= 
+ 
= 
+ = 
(where and are the field intensity of plate A and B respectively).
If V is the potential difference between the plates then, V = E.d = 
.
The capacitance of the parallel plate capacitor C = = 
= 
.
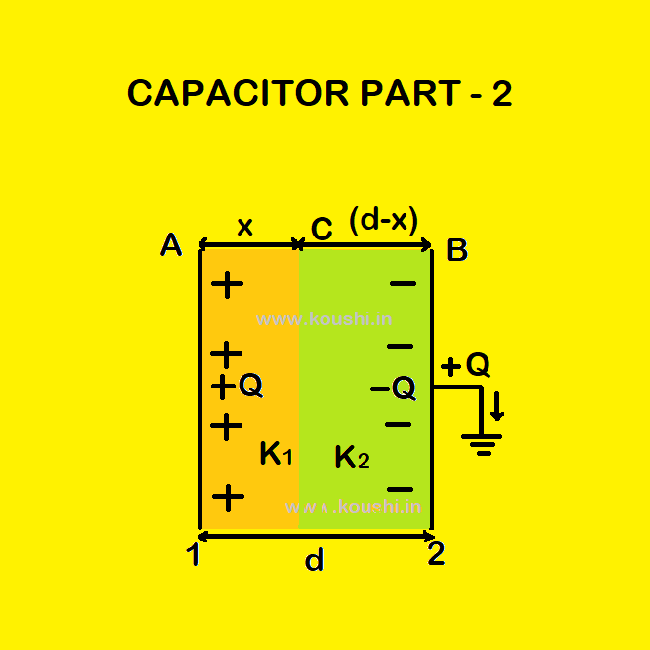
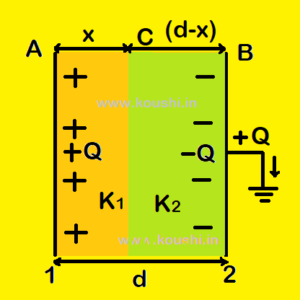
Capacitance of a parallel plate capacitor (with dielectric):
Let us consider a parallel plate capacitor consists of two parallel plates (A and B) each of plate area A and the separation between the plates is d. A plate is charged by Q and the outer surface of B is earthed. So, –Q charge is induced in the inner surface of B.
Let two dielectric medium of dielectric constant K1 and K2 of thickness x and (d-x) respectively introduced in between the plates as shown in figure.
The electric field between AC and CB are respectively E1 = 
= 
and E2 = 
= 
(where σ is the surface charge density of each plate).
The potential difference between AC is VA – VC = E1.x = 
And the potential difference between CB is VC – VB = E2(d-x) = 
If V is the potential difference between the plates then, V = (VA – VC) + ( VC – VB)
Or, V = 
Or, V = 
The capacitance of the parallel plate capacitor C = = 
.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.