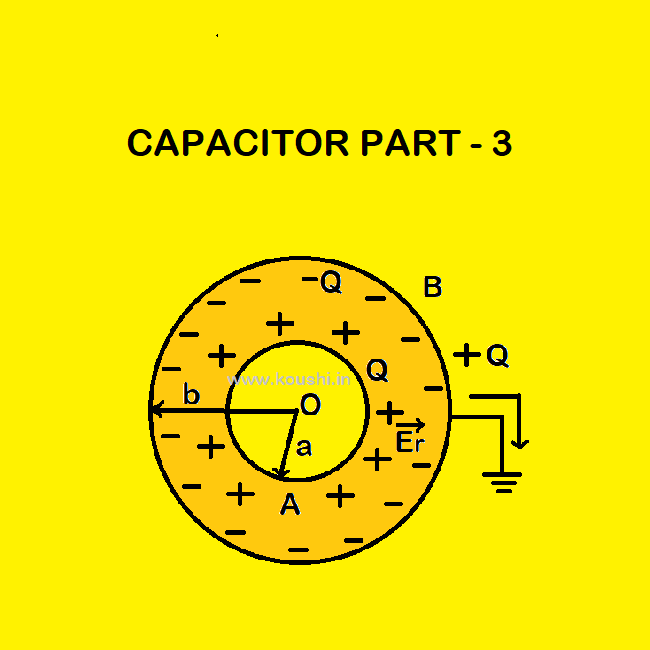
Capacitance of a spherical capacitor (outer sphere is earthed):
Let us consider A and B are the two concentric spherical shells of radii a and b respectively (b >a). Shell A is charged by Q and the outer surface of shell B is earthed. So –Q charge is induced in the inner surface of B.
If 
is the electric field between the shells at a distance r from the centre then 
.
= 
or, E = 
(using Gauss’s law).
We know that dV = – .
= – 
(Angle between and is 00)
On the surface of A potential is V and that on the surface of B is 0 as it is earthed. If V is the potential difference between the shells then, 
dV = – 
Or, – V = – |- 
Or, – V = [
– 
]
Or, V = [
]
The capacitance of the spherical plate capacitor C = 
= 
= 
.
Capacitance of a spherical capacitor (inner sphere is earthed):
Let us consider A and B are the two concentric spherical shells of radii a and b respectively (b >a). Sphere B is charged by q and the outer surface of A is earthed, so VA = 0.
If q/ charge is induced on shell A then, k[ 
+ 
] = 0 or, q/ = – 
.
If is the electric field between the shells at a distance r from the centre then
E = EA + EB = 
+ 0 [EB = 0 as E is outward for shell B]
E = – 
= k[- ]
Or, 
dV= 
dr
Or, V = |- 
Or, V = [ – ]
Or, V = 
The capacitance of the spherical plate capacitor C = 
= 
.
Combination of spherical capacitors:
Three concentric conducting spheres A, B and C each of radii a, b and c respectively filled with air. Sphere B is earthed and sphere A and C are connected with a wire. Calculate the equivalent capacitance.
This combination is the parallel combination of two spherical capacitors as the potential of sphere A and sphere C are same. (i) 1st capacitor is formed with sphere A and the inner surface of sphere B of capacitance C1 =
(ii) 2ndcapacitor is formed with outer surface of sphere B and inner surface
of sphere C of capacitanceC2 = 
.
So, the net capacitance is C = C1 + C2 = + = 
.
Capacitance of a cylindrical capacitor:
Let us consider A and B are the two coaxial cylinders of radii a and b respectively (b > a) each of length l. Cylinder A is charged by Q and the outer surface of B is earthed. So –Q charge is induced in the inner surface of B. If is the electric field between the cylinders at a distance r from the axis then, . 
.
Or, E = 
(using Gauss’s law).
We know that dV = – . = – 
. [Angle between and is 00 ]
On the surface of A potential is V and that on the surface of B that is 0 as it is earthed. If V is the potential difference between the cylinders then, dV = – 
dr
Or, – V = – |
Or, V = 
.
The capacitance of the spherical plate capacitor C = = 
.
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.