Application of Circular Motion
1. A conical funnel rotates about its own axis with angular speed 
. A particle remain stationary on the inner surface of the funnel and it describes a horizontal circular motion of radius r as shown in figure. The coefficient of friction between particle and inner surface of the funnel is 
. What is the minimum value of , so that the particle remain stationary on the inner surface of the funnel.
As the funnel rotates with angular speed , then it is considered as accelerated frame. Therefore, the particle experiences a pseudo force 
due to it. Let us consider, R is the normal reaction between particle and funnel. The frictional force between the particle and funnel acts along the inner surface of funnel in the upward direction to hold it at that position.
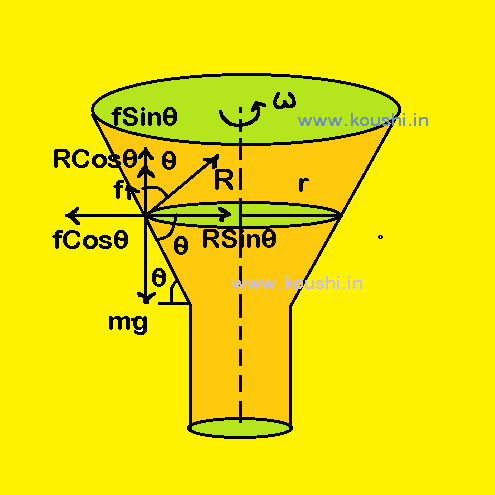
Therefore, Rcos
+ fsin = mg
Or, Rcos + Rsin = mg —– (i)
And Rsin – fcos =
Or, Rsin – Rcos = —- (ii) [when we observe from ground i.e. inertial frame of reference, the particle rotates due to the centripetal force.]
Dividing equation (ii) from equation (i) we get, 
= 
= 
=
.
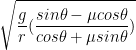2. A mass m is released from the top of a hemisphere (point P) of radius r with horizontal speed v. Calculate the angle with respect to the vertical where it leaves the contact from the hemisphere.
Let us consider, the mass will leave the contact from the hemisphere at point Q. If R is the reaction force acts on the mass by the hemisphere, then mgcos – R provides the required centripetal force to the mass during its circular motion. If at point Q, the speed of the mass is u, then mgcos – R = 
.
When the mass leaves the contact from the hemisphere, then R = 0, so, mgcos = .
cos = 
—– (i)
We draw a perpendicular QS on PO. Therefore, SO = h = rcos .
Using conservation of energy at point P and Q we get, 
+ mg(PS) = 
Or, + mg(r- rcos) =
Or, 
= 
+ 2gr(1- cos)
u = 
Putting the value of u in equation (i) we get, cos = 
Or, cos = 
+ 2 – 2cos
Or, 3cos = + 2
= 
.
4. A liquid is kept in a cylindrical vessel of radius r which is rotated about its axis with angular speed . Find the difference in the height of the liquid at the centre of the vessel and its side.
We consider a point mass m at point P (x, y) on the surface of the liquid. R is the reaction force acts on the point mass by the surface of liquid, then Rcos = mg —– (i)
And Rsin = 
——- (ii)
Therefore, tan = 
—– (iii)
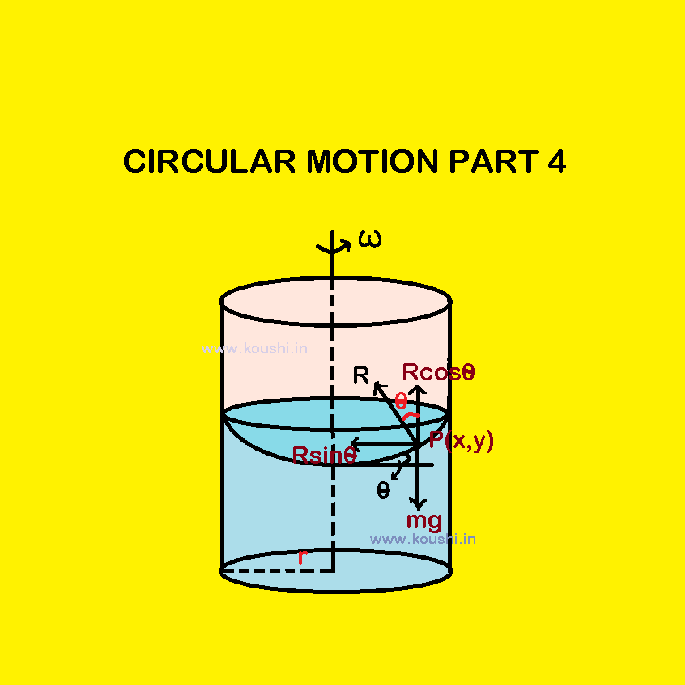
But tan = slope = 
—— (iv)
From equation (iii) and (iv) we get, =
Or, dy = 
Or, 
dy = 
[h is the difference in the height of the liquid at the centre of the vessel and its side]
h = 
.
5. Three particle of mass m are placed at three vertexes of an equilateral triangle of each side a. If the system rotates about the centroid due to the mutual gravitational force, then calculate the velocity.
The gravitation force of attraction acting on each mass due to other is F = 
.
The net gravitation force is F/ = 
= 
= 
.
As the system rotates about the centroid due to the mutual gravitational force, then net gravitation force provides the required centripetal force for rotation.
So, = 
= 
. [AO = 
AD = 
= 
= 
]
v = 
.
6. A metal ring of mass m and radius r is rotated on a plane frictionless surface about its centre in such a way that each part of the ring moves with speed v. Find the tension on the ring.
The mass per unit length of the ring is 
. We consider an elementary part of the ring of length dl [
= r]. Mass of that part is dm = 
= 
= 
. If T is the tension of the ring, then the vertical component of tension provides the required centripetal force for rotation. So, 2Tsin = 
Or, 2T = 
[as 
, then sin = ]
T = 
.
7. A smooth rod of length L can rotate in a horizontal plane about an axis passing through its one end perpendicularly. A frictionless ring is placed at a distance l from the axis of the rod. If the rod is rotated with angular speed , then calculate the horizontal velocity of the ring with respect to ground when it leaves the other end of the rod.
[The angular momentum of the system remains unchanged during the displacement of the ring]
Let us consider the mass of the ring is m. At any instant the ring is at a distance x from the axis of the rod during rotation. The centrifugal force acting on the ring is F = 
.
The work done required to move the rod for small displacement dx is dw = dx.
The total work done required to move the rod form l to L is 
dw = 
dx
Or, w = 
This work done is equal to change in kinetic energy.
Therefore, =
v = 
The tangential velocity of the ring is vT = L .
Therefore, net horizontal velocity of the ring is 
= 
.
8. A bob of mass m is suspended from a celling by a massless inextensible string of length l. The bob is now rotated in a horizontal circular path. Calculate the speed of the bob so that the tension of string is T.
Let the speed of the bob is v. Tcos = mg —- (i) and Tsin = 
—-(ii)
From equation (i) and (ii) we get, sin2 + cos2 = 
+ 
Or, = 1 –
v = 
.
tag:
Share:
Admin Koushi
