Circular Motion Part 4

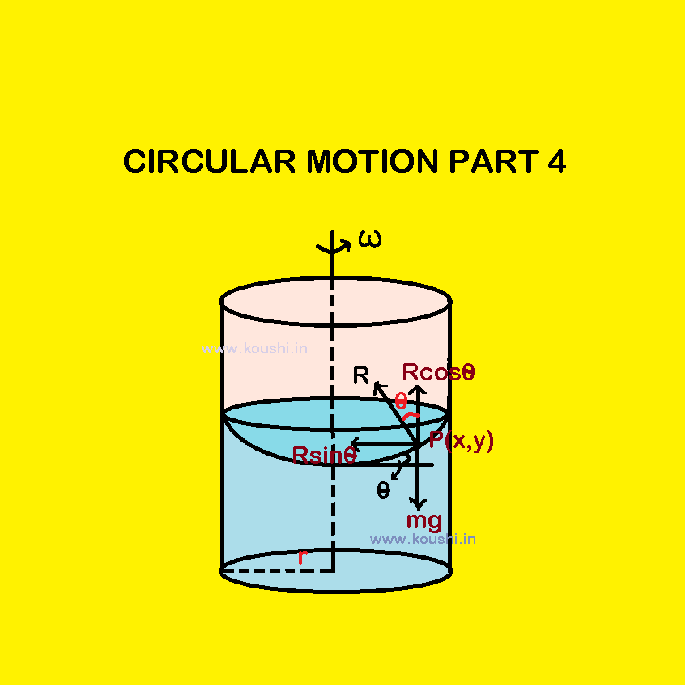
4. A liquid is kept in a cylindrical vessel of radius r which is rotated about its axis with angular speed . Find the difference in the height of the liquid at the centre of the vessel and its side.

We consider a point mass m at point P (x, y) on the surface of the liquid. R is the reaction force acts on the point mass by the surface of liquid, then Rcos = mg —– (i)

And Rsin = ——- (ii)

Therefore, tan = —– (iii)

But tan = slope = —— (iv)

From equation (iii) and (iv) we get, =

Or, dy =

Or, dy = [h is the difference in the height of the liquid at the centre of the vessel and its side]

h = .

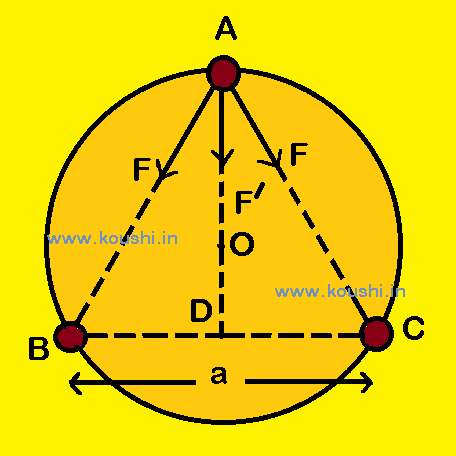
5. Three particle of mass m are placed at three vertexes of an equilateral triangle of each side a. If the system rotates about the centroid due to the mutual gravitational force, then calculate the velocity.

The gravitation force of attraction acting on each mass due to other is F = .

The net gravitation force is F^/ = = = .

As the system rotates about the centroid due to the mutual gravitational force, then net gravitation force provides the required centripetal force for rotation.

So, = = . [AO = AD = = = ]

v = .

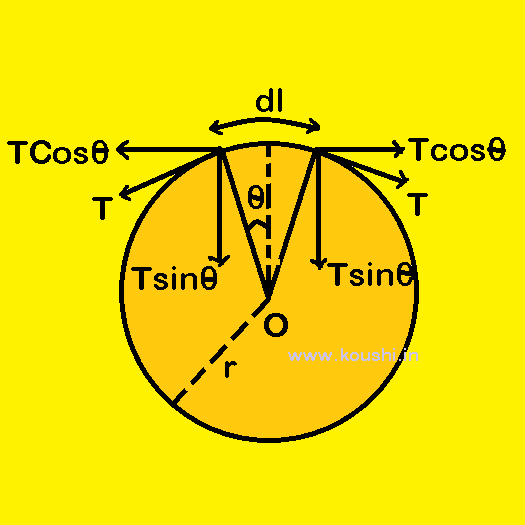
6. A metal ring of mass m and radius r is rotated on a plane frictionless surface about its centre in such a way that each part of the ring moves with speed v. Find the tension on the ring.

The mass per unit length of the ring is . We consider an elementary part of the ring of length dl [ = r]. Mass of that part is dm = = = . If T is the tension of the ring, then the vertical component of tension provides the required centripetal force for rotation. So, 2Tsin =

Or, 2T = [as , then sin = ]

T = .

7. A smooth rod of length L can rotate in a horizontal plane about an axis passing through its one end perpendicularly. A frictionless ring is placed at a distance l from the axis of the rod. If the rod is rotated with angular speed , then calculate the horizontal velocity of the ring with respect to ground when it leaves the other end of the rod.

[The angular momentum of the system remains unchanged during the displacement of the ring]

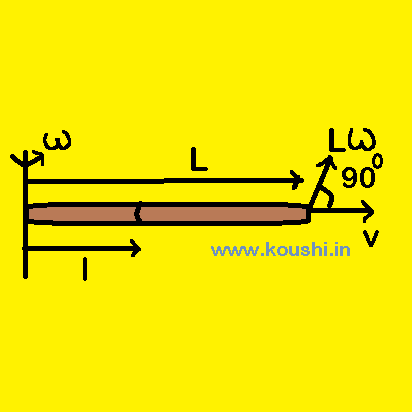
Let us consider the mass of the ring is m. At any instant the ring is at a distance x from the axis of the rod during rotation. The centrifugal force acting on the ring is F = .

The work done required to move the rod for small displacement dx is dw = dx.

The total work done required to move the rod form l to L is dw = dx

Or, w =

This work done is equal to change in kinetic energy.

Therefore, =

v =

The tangential velocity of the ring is v_T = L .

Therefore, net horizontal velocity of the ring is = .

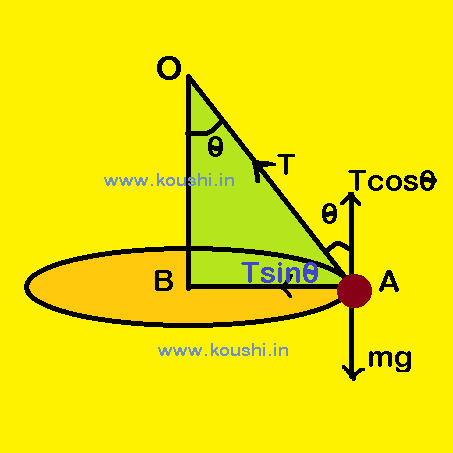
8. A bob of mass m is suspended from a celling by a massless inextensible string of length l. The bob is now rotated in a horizontal circular path. Calculate the speed of the bob so that the tension of string is T.

Let the speed of the bob is v. Tcos = mg —- (i) and Tsin = —-(ii)

From equation (i) and (ii) we get, sin² + cos² = +

Or, = 1 –

v = .