Differential calculus in physics
Learn differential calculus in physics with key concepts, formulas, and applications to motion, velocity, and acceleration. Ideal for NEET, JEE Main, and JEE Advanced preparation.
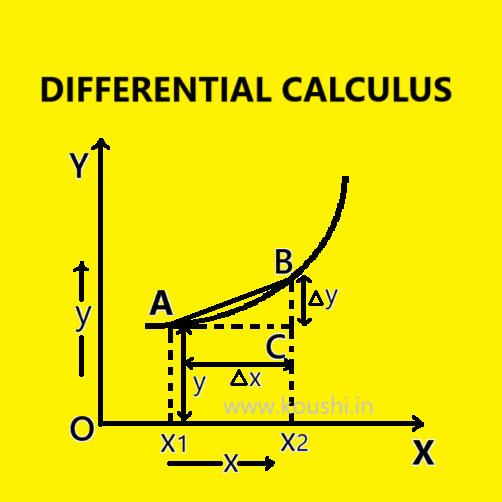
Let us consider, a physical quantity y depends on another physical quantity x i.e., y = 
.
The graph shown in figure represents the variation of y with respect to x and A and B are two points on the graph. We draw two perpendiculars on OX from point A and B.
AC and BC are two mutually perpendiculars which represents the small change in x i.e 
x and corresponding change in y i.e y respectively.
The rate of change of y with respect to x is 
= slope of the line AB = tan
.
But the rate of change is not same at all points on the graph because at point B the slope is more. Therefore, to get the rate of change of y with respect to x at point A, x should be very small and points A and B are very close.
The slope or the tangent at point A gives the rate of change of y with respect to x at point A is 
= 
. Where 
is the differentiation operator.
Some common formulas of differentiations are respectively:
(i) | (ii) |
(iii) | (iv) |
(v) | (vi) |
(vii) | (viii) |
(ix) | (x) |
= cosx
= - sinx
= secxtanx
= - cosecxcotx
Some common rules of differentiations are respectively:
(i) 
where A is a constant.
If u and v are then,
(ii) 
(iii) 
(iv) 
(v) 
(vi) 
this is known as chain rule.
Click the YouTube button to get the video (English) explanation of differential calculus.
This video contains:
- Where differential calculus is used?
- How to use differential calculus?
- Major mistakes done by the students to apply diferential calculus.
Applications of differential calculus to solve physics problems:
1. The velocity-displacement graph of a particle is given in figure. What is the acceleration when displacement is 2 m?
From the graph, slope is 
= tan300 = 
Acceleration of the particle is a = 
= ( )( 
) = v( ) = 
When s = 2 m then, v = 3 ms-1. ∴ a = = 
= 
ms-2.
2. One dimensional motion of body:
A particle is moving in a straight line and its displacement is x = (3t3 – 1.5t2 + 2) m. What is the velocity and acceleration of the particle in 2 s? What is the displacement when velocity of the particle is zero?
Velocity of the particle is v = 
= 
= 9t2 – 3t. At t = 2 s v = 30 ms-1.
Acceleration of the particle is a = = 
= 18t – 3. At t = 2s a = 33 ms-2.
Now v = 0 so, 9t2 – 3t = 0 or, t = 
s. At t = s displacement is x = 3
– 1.5
+ 2 = 
m.
3. Pulley problem using differential calculus:
A ring initially at rest can slide downward through a smooth vertical wire. The ring is connected with a block by a massless inextensible string through a fixed pulley as shown in figure. What is the ratio of velocities of ring and the block if the string creates an angle 
at pulley with the initial horizontal position?
Let us consider, when string creates angle , the vertical downward displacement of ring is x and the block is at a distance y from pulley. The distance between vertical wire and pulley is l which remain constant.
The length of the string is L = 
+ y = constant
The velocity of the ring is 
= and the velocity of the block is 
= – 
(taking downward motion is positive and upward motion is negative)
Now, 
+ = 
Or, 
× 2x + = 0
Or, (sin ) =
∴ 
= cosec .
4. Pulley 1 is fixed and block A is connected by a massless inextensible string with a movable pulley 2 as shown in figure. Another block B is connected with a string over the pulley 2 and the other end of the string is fixed with horizontal surface. Mass of block B is more than that of block A. What is the relation of acceleration of block A and block B?
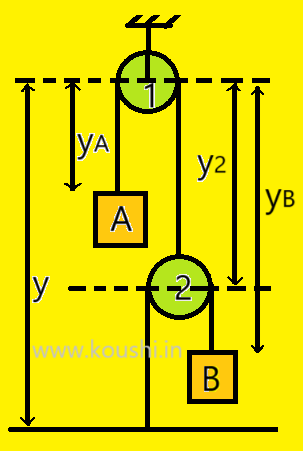
We consider a horizontal reference line through the centre of pulley 1. The distance of block A, pulley 2, block B and horizontal surface at bottom from that line are respectively 
, 
, 
and y.
If 
is the length of the string over pulley 1 and 
is the total length of string which connects body A and pulley 2 then, + + =
Differentiating the equation with respect to time t we get, 
+ 
+ 
= 
Or, – 
+ 0 + 
= 0 (as and are constant, then differentiation is 0 and taking upward motion is negative)
Or, =
Or, 
= 
Or, 
= 
—– (1)
If 
is the length of the string over pulley 2 and 
is the total length of string connected between body B and horizontal surface then,
(y – ) + + (
– ) =
Or, y – 2 + + =
Differentiating the equation with respect to time t we get, 
– 2
+ 
+ 
= 
Or, 0 – 2 + 0 + 
= 0 (as and are constant then differentiation is 0)
Or, = 2
Or, 
= 2
Or, 
= 2
—— (2)
From equation (1) and (2) 2
= .
tag:
Share:
Admin Koushi
