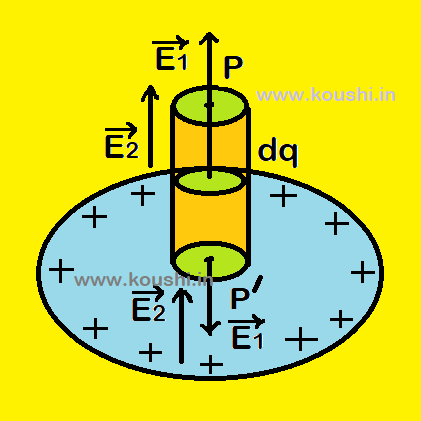
Force per unit area of a charged conductor:
Let us consider the electric field E at any point P very near, but outside, the surface of a charged conductor is E = E1 + E2. Where E1 is the field due to the charge of small area ds around P, and E2 due to the charge on the rest of the surface.
Consider a point P’ opposite to P near the surface, but inside the conductor. For the point P’ the electric field E = E1 – E2 = 0.
So, E1 = E2 = 
. The electric field near the surface of a charged conductor is E = 
. Where 
 is the surface charge density.
The force acting on the charge ds due to the charges of rest of the surface is F = dsE2 = 
.
Force per unit area of a charged conductor is 
 = 
 = 
.
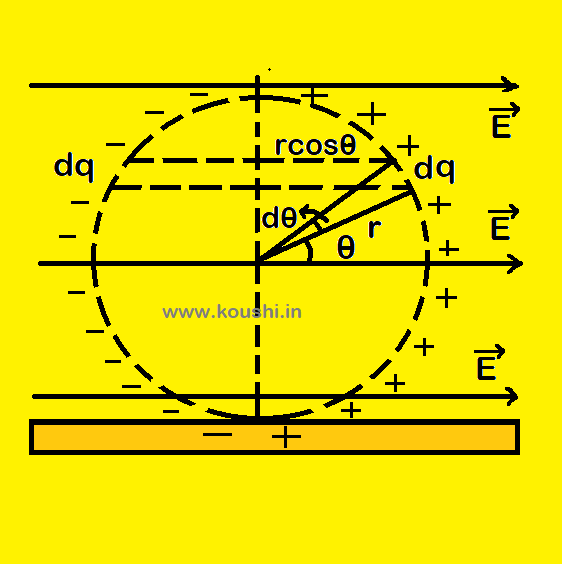
Dipole moment on a charged ring:
A nonconducting ring of mass m radius r is vertically rest on a smooth non conducting horizontal plane. Charges +q and -q is distributed uniformly on the ring. Let dq is the charge at an angle 
for elementary part dl of the ring. So, dq = λrdθ. The dipole moment for dq on both side of the ring is dP = dq2r cos = λrdθ2r cos = 2λr2 cos dθ.
The net dipole moment for the entire ring is
P = 
 = 2λr2 
cos d  = 2λr2[sin 
 = 4λr2 =4r2(
) = 
.
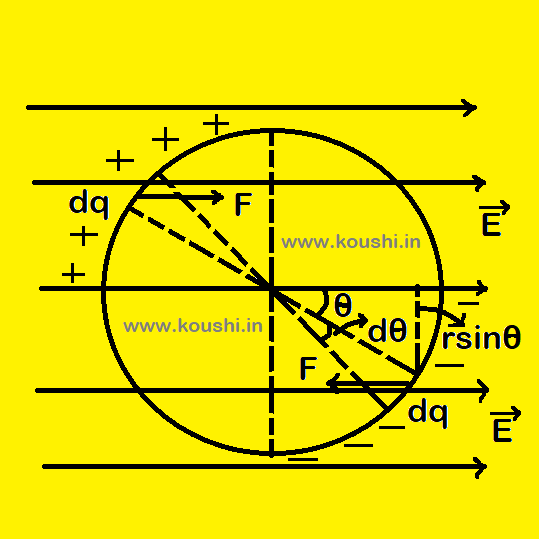
The torque acting on the ring in electric field:
A nonconducting ring of radius r is vertically rest on a smooth non conducting horizontal plane. Charges +q and -q is distributed uniformly on 
th part of the ring as shown in figure. A uniform electric field E is set up parallel to the horizontal plane. Let dq is the charge at an angle  for elementary part dl of the ring.
So, dq = λrdθ. Force acting on dq is dF = dqE = λrdθE.
The torque due to E is d
= dF2r sin = 2λr2E sin dθ
The torque acting on the ring is  = 
= 2λr2E 
sin d  = 2λr2E = 2Er2( 
) = 
.
Click the button to go to the previous part of this chapter.