

Electric charges and field Part – 12
tag:
Share:
Admin Koushi


Concept of conductor:
1. Electric field at the surface of a conductor:
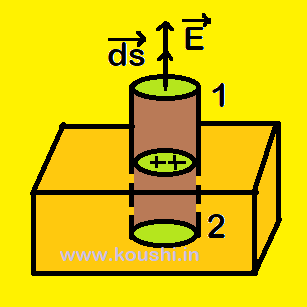
Let us consider an elementary surface ds of a conductor of surface charge density ![]() . The surface is enclosed by a cylindrical Gaussian surface which is inside and outside of the conductor. As the electric field is perpendicular to the surface so flux for the surface 1 is
. The surface is enclosed by a cylindrical Gaussian surface which is inside and outside of the conductor. As the electric field is perpendicular to the surface so flux for the surface 1 is ![]() =
= ![]() .
.![]() = Eds.
= Eds.
Electric field inside the surface of a conductor is zero. So flux for the surface 2 is ![]() = 0.
= 0.
So, net flux through the elementary surface ds is d![]() = Eds.
= Eds.
Using Gauss’s law, ![]() =
= ![]() d
d![]() =
= ![]() Eds =
Eds = ![]()
Or, ES = ![]() so, E =
so, E = ![]() =
= ![]() .
.
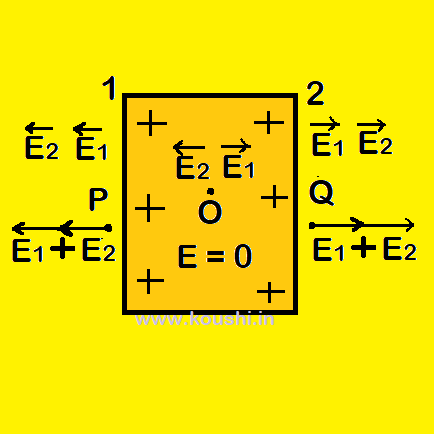
2. Electric field due to a charged isolated conducting plate: The electric field due to a charged isolated conducting plate is twice the field due to a plane sheet of charge. The electric field due to charged sheet 1 and 2 are E1 = ![]() and E2 =
and E2 = ![]() .
.
The electric field at point P is EP = E1 + E2 = ![]() .
.
The electric field at point Q is EQ = E1 + E2 = ![]() .
.
The electric field at point O is EO = E1 – E2 = 0.
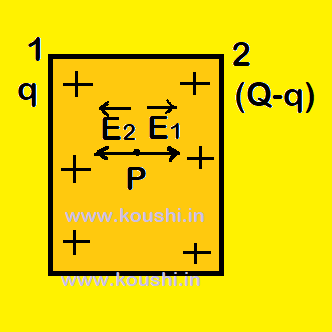
3. The charge is distributed equally on two surfaces of an isolated large conducting sheet:
Let us consider Q is the total charge of the conducting sheet where q is on surface 1 and (Q – q) is on surface 2.
The electric field at point P due to surface 1 is E1 = ![]() .
.
The electric field at point P due to surface 2 is E2 = ![]() .
.
The net electric field at point P is E1 – E2 = ![]() –
– ![]() = 0 [as the electric field inside a conductor is zero]
= 0 [as the electric field inside a conductor is zero]
So, q = Q – q
![]() q =
q = ![]() Q.
Q.
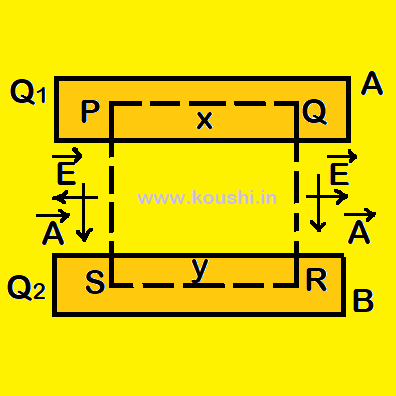
4. The charges on the inner surfaces of two parallel conducting plates A and B having charge Q1 and Q2 respectively are equal and opposite sign:
Let us consider x and y are the charges of the inner surfaces of conducting plates A and B. We consider a Gaussian surface as shown in figure. For the surfaces PS and QR the area vector and electric field are perpendicular, so the flux through these surfaces is zero. The surfaces PQ and RS are inside the conductor so electric fields through these surfaces are zero and flux also zero. So the net flux through surface PQRS is zero. Using Gauss’s law ![]() = 0
= 0
![]() x = – y.
x = – y.
5. Charges appear on the surfaces of two parallel conductors: Let us consider q1 and q2 are the charges of two identical metal plates each of surface area A. If x and -x are the charges of the inner surfaces 2 and 3 of conducting plates A and B respectively then charge of surfaces 1 and 4 are(q1 –x) and (q2 + x).
The surface charge density of surfaces 1, 2, 3 and 4 are respectively ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() and
and ![]() =
= ![]() .
.
The net electric field at point P is E1 – E2 + E3 – E4 = 0 or, ![]() –
– ![]() +
+ ![]() –
– ![]() = 0
= 0
Or, ![]() +
+ ![]() =
= ![]() +
+ ![]() or, (q1 –x) + x = x + (q2 + x) Or, x =
or, (q1 –x) + x = x + (q2 + x) Or, x = ![]() .
.
Therefore charges of surfaces 1, 2, 3 and 4 are respectively ![]() ,
, ![]() , -(
, -(![]() ) and
) and ![]() .
.
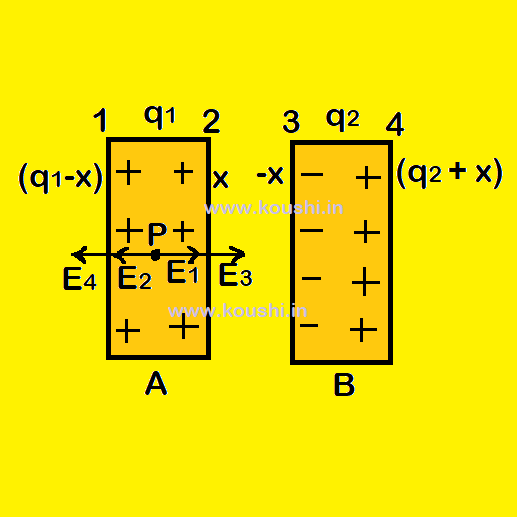
Facing surfaces have equal but opposite nature of charges with magnitude half the difference of the charges of the plates.
The outer surfaces always have equal charges of magnitude half the summation of charges of the plates.
The charge appearing on surfaces 2 and 3 are called bounded charge, and the charge appearing on surfaces 1 and 4 are called free charge.
If the second plate is connected with ground, the charge appearing on surface 4 will go to the earth.
6. Charges appear on the surfaces of three parallel conductors: Let us consider q1, q2 and q3 are the charges of three identical metal plates each of surface area A. If x and -x are the charges of the surfaces 2 and 3 of conducting plates A and B respectively then charge of surfaces 1 and 4 are (q1 –x) and (q2 + x).
The surface charge density of surfaces 1 and 2 are respectively ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
The net electric field at point P, inside plate A is E1 – E2 – EB – EC = 0
Or, ![]() –
– ![]() –
– ![]() –
– ![]() = 0
= 0
Or, ![]() –
– ![]() –
– ![]() –
– ![]() = 0
= 0
Or, q1 –x = x + q2 + q3
Or, x = ![]() .
.
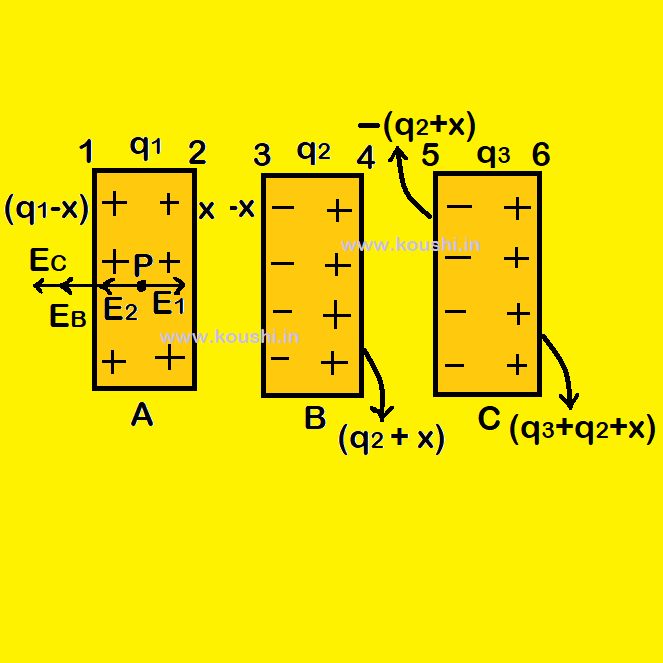
Therefore, charge of surfaces 1 is q1 – x = q1 – (![]() ) =
) = ![]() .
.
Charge of surfaces 2 is x = ![]() and charge of surfaces 3 is – x = –
and charge of surfaces 3 is – x = – ![]() .
.
Therefore, charge of surfaces 4 is q2 + x = q2 + ![]() =
= ![]() and charge for surface 5 is – (
and charge for surface 5 is – (![]() ) .
) .
Therefore, charge of surfaces 6 is q2 + q3 + ![]() =
= ![]() .
.
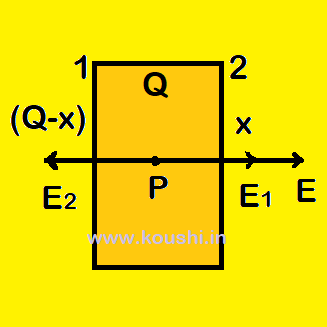
7. Charges appearing on two surfaces of a conducting sheet of area A charge Q is placed perpendicular to the electric field E:
Let us consider x charge on surface 2 and Q – x is on surface 1. The surface charge density of surfaces 1 and 2 are respectively ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
The net electric field at point P, inside plate is E1 – E2 + E = 0
Or, ![]() –
– ![]() + E = 0
+ E = 0
Or, ![]() –
– ![]() + E = 0
+ E = 0
Or, Q – x – x + ![]() = 0
= 0
![]() x =
x = ![]() Q + A
Q + A![]() E.
E.
So, charge on surface 1 is (![]() Q – A
Q – A![]() E).
E).
Click the button to go to the next part of this chapter.
Click the button to go to the previous part of this chapter.
© 2018 – 2025 Koushi All Rights Reserved