Equations of Motion

1. Prove v = u + at: Let us consider a particle is moving with uniform velocity u. Then it accelerates uniformly with a and after time t its final velocity is v. The change in velocity is (v – u) for time t. The acceleration of the particle is a .

Or,

Or, at = v – u

2. Prove : Let us consider a particle is moving with uniform velocity u. Then it accelerates uniformly with a and after time t its final velocity is v. The distance travelled by it for time t is s.

The average speed of the particle during its motion is .

Then,

Or,

Or, [as v = u +at]

3. Prove v² = u² +2as: Let us consider a particle is moving with uniform velocity u. Then it accelerates uniformly with a and after time t its final velocity is v. The distance travelled by it for time t is s.

We know that, v = u + at

Or, v² = (u + at)²

Or, v² = u² +2uat + a²t²

Or, v² = u² + 2a(ut + )

v² = u² + 2as [as s = ut + ].

4. The distance traveled by a particle in second: Let us consider a particle is moving with uniform velocity u. Then it accelerates uniformly with a and after time n second the distance travelled by it is .

The distance travelled by it in (n-1) second is .

The distance travelled by it in second is

Or, = un – u(n – 1) + —

Or, = u +

= u + .

Concept on inclined plane: A ball is released downwards from the top of a frictionless inclined plane of inclination . What is the speed of the ball when it travels l distance on inclined plane? Also calculate the time to travel distance l.

The acceleration of the ball on inclined plane is . The speed of the ball when it travels l distance on inclined plane is v. Then, .

v = [as u = 0].

If t is the time taken to travel distance l, then using the relation s = ut + at² we get,
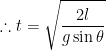