Defects of vision of human eye: The most distant point which an eye can see clearly is called the far point (F). For the normal eye the far point lies at infinity. The nearest point which an eye can see clearly is called the near point (N). For normal eye, near point lies at a distance between 20 cm to 30 cm. Conveniently N is taken at a distance of 25 cm. This is known as least distance of distinct vision and it is denoted by D.
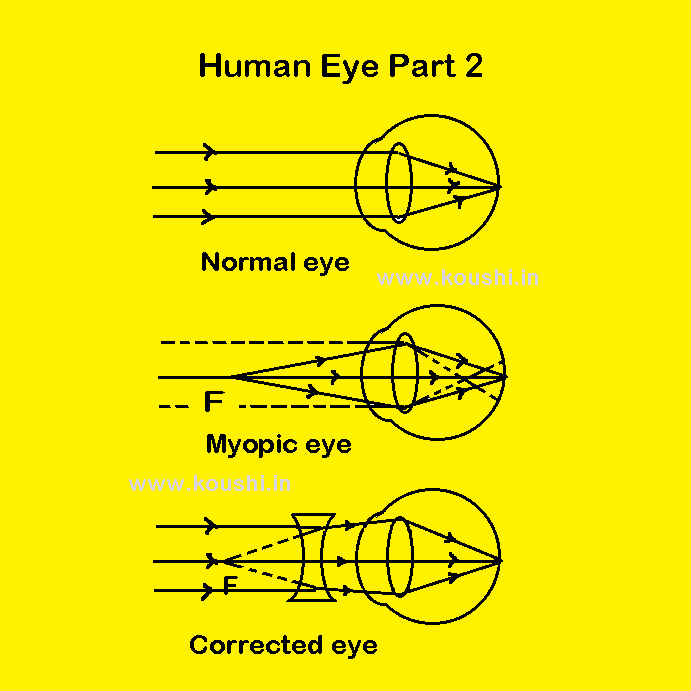
Myopia or short-sightedness: A myopic person can distinctly detect the object which is near, but he cannot see distinctly the far objects which are lying beyond a certain distance.
Due to this defect the far point of the eye shifts towards the eye from infinity.
Cause of myopia: 1. The elongation of eyeball
- The decrease in the focal length of eye lens or if the lens becomes thicker.
Correction of myopia: To correct myopia, a concave lens of such a focal length is placed infront of eye, so that the rays coming from infinity should appear to come from the far point (F) of myopic person. Therefore, the rays coming from infinity can be focused at the retina.
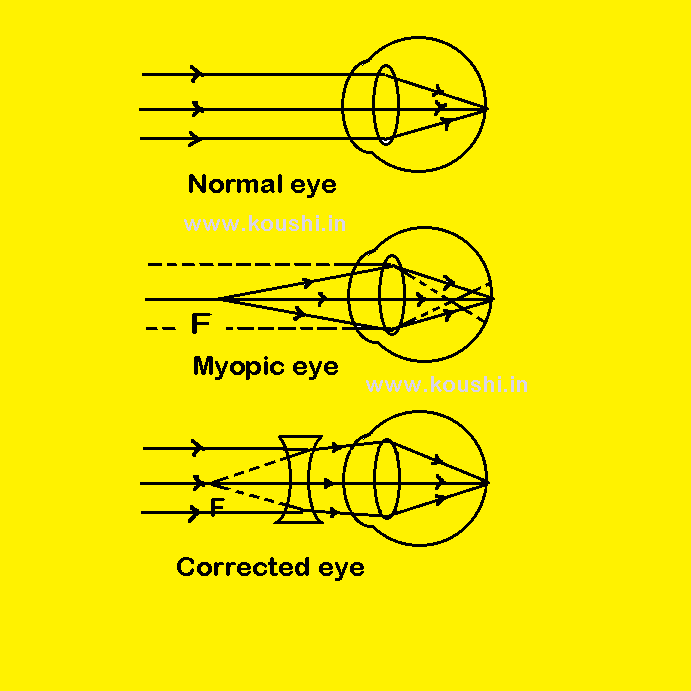
Let us consider x is a distance of F from myopic eye. The focal length of lens used is f.
Then using lens formula, we get, ![]() –
– ![]() =
= ![]()
Or, ![]() =
= ![]() –
– ![]()
![]() f = – x
f = – x
[- ve sign indicates that the lens ie required here concave].
Hypermetropia or longsightedness: A hypermetropic person can distinctly detect the far off object, but cannot see distinctly the near objects which are lying nearer than a certain distance.
For a normal eye, the least distance is 25 cm (denoted by D), but for hypermetropic person, near point is beyond 25 cm.
Cause of hypermetropia: 1. Contraction of the eyeball
- Increase in the focal length of eye lens or lens become thinner.
Correction of hypermetropia: It can be corrected by a convex lens of proper focal length, is placed in front of eye, so that the object at a distance D, should appear to come from the near point of hypermetropic person.
Therefore, the rays coming from the least distance (D) can be focused at the retina.
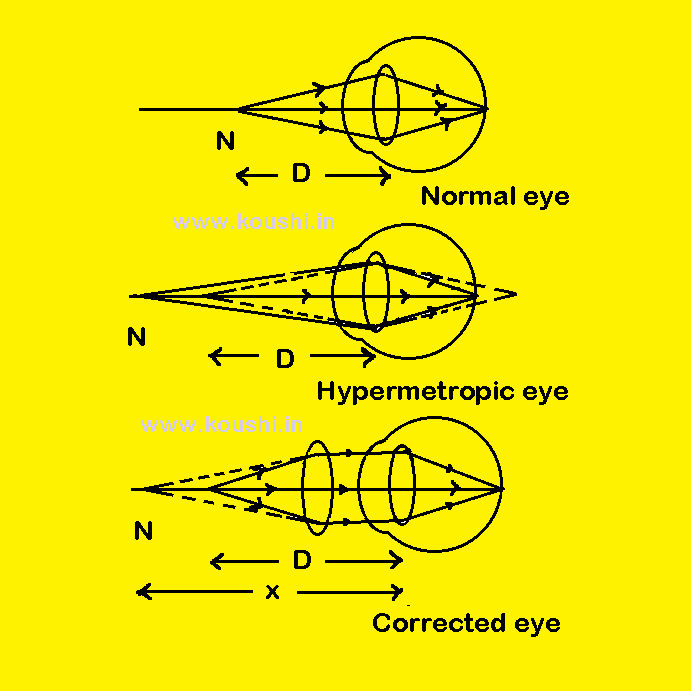
Let us consider the near distance of hypermetropic eye is x.
The least distance of distinct vision is D.
Therefore, object distance u = – D, image distance (virtual) v = – x. If f is the focal length of required convex lens, then using lens formula we get, ![]() –
– ![]() =
= ![]()
Or, ![]() =
= ![]() –
– ![]() =
= ![]() –
– ![]() =
= ![]()
![]() f =
f = ![]()
[The positive value of f indicates that the required lens is convex].