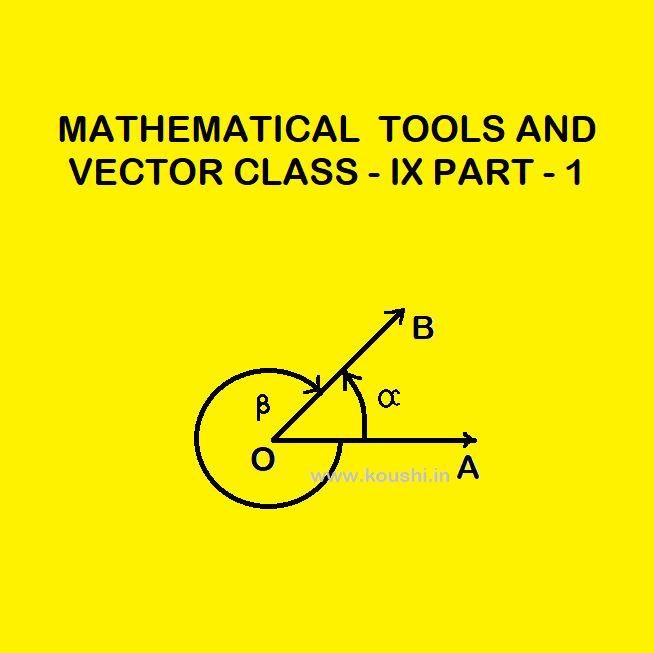
CONCEPT OF TRIGONOMETRY:
Trigonometry is the part of mathematics where we learn about the angle. We know that in geometry the measured angle is restricted in between ![]() to
to ![]() and it is positive. But in trigonometry there is no limit of angle and it may be positive or negative.
and it is positive. But in trigonometry there is no limit of angle and it may be positive or negative.
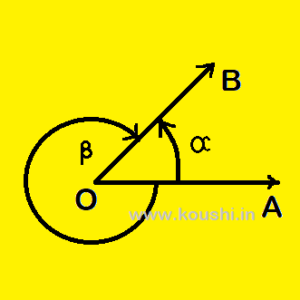
Let us consider OA and OB are two straight lines initially coincide with each other. OB rotates about point O and creates angle ![]() keeping OA fixed. If OB rotates in anticlockwise direction then
keeping OA fixed. If OB rotates in anticlockwise direction then ![]() =
= ![]() is positive. If OB rotates in clockwise direction then
is positive. If OB rotates in clockwise direction then ![]() =
= ![]() is negative.
is negative.
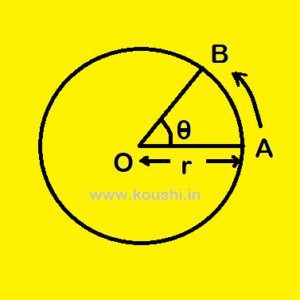
CIRCULAR SYSTEM OF MEASURING ANGLE:
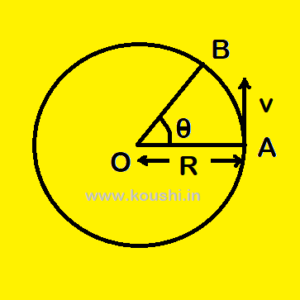
A particle rotates in a circular path of radius OA (=r) in anticlockwise direction. The particle is at point B creates an angle ![]() =
= ![]() .
.
The angle subtended at the centre of the circle by arc is the ratio of length of arc to the radius of the circle. ![]() =
= ![]() =
= ![]() .
.
In circular system the unit of angle is radian. The angle subtended at the centre of the circle by arc whose length is equal to the radius of the circle is called one radian.
RELATION BETWEEN RADIAN AND DEGREE:
A particle rotates in a circular path of radius r and completes one rotation. Then angle subtended at the centre is ![]() =
= ![]() .
.
In radian unit ![]()
![]() =
= ![]() =
= ![]() .
.
Therefore, ![]() radian =
radian = ![]()
Or, 1 radian = ![]() =
= ![]() =
= ![]()
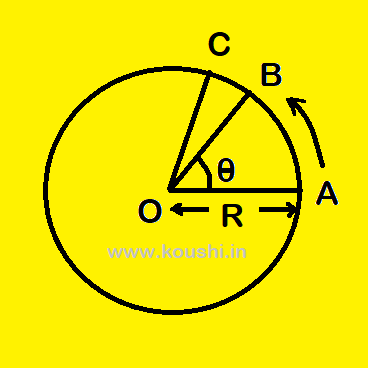
PROVE ![]() =
= ![]() :
:
Let us consider a particle rotates in a circular path of radius R in anticlockwise direction starting from point A. The particle is at
point B creates an angle ![]() =
= ![]() . The length of arc AB = S.
. The length of arc AB = S.
So, ![]() =
= ![]() ——–(i)
——–(i)
Now we consider another point C on the circumference of the circle so that AC = R. Therefore the angle ![]() = 1 radian. So,
= 1 radian. So, ![]() =
= ![]() ——–(ii)
——–(ii)
As angle subtended at the centre of a circle is directly proportional to its arc, then from equation (i) and (ii) we get, ![]() =
= ![]()
Or, ![]() =
= ![]()
![]()
![]() =
= ![]() [where
[where ![]() is measured in circular system].
is measured in circular system].
APPLICATION IN PHYSICS:
A particle rotates in a circular path of radius r in anticlockwise direction. If the linear speed of the particle is v then what is its angular speed?
Let us consider the particle starting from point A and comes at point B and the ![]() =
= ![]() . Length of arc AB = S and the time of travel is t. So, v =
. Length of arc AB = S and the time of travel is t. So, v = ![]() .
.
Angular speed of the particle is ![]() =
= ![]() =
= ![]() [as
[as ![]() =
= ![]() ] Or,
] Or, ![]() =
= ![]() (
(![]() ) =
) = ![]() .
.
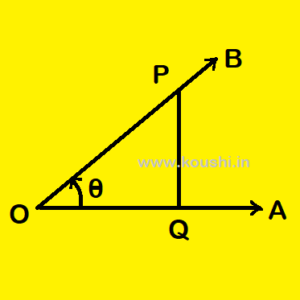
TRIGONOMETRICAL RATIO OF POSITIVE ACUTE ANGLE:
Let us consider, OA and OB are two straight lines initially coincide with each other. OB rotates about point O and creates angle ![]() =
= ![]() keeping OA fixed. P is a point on OB and PQ is perpendicular on OA. Therefore, OQ is base, PQ is perpendicular and OP is the hypotenuse of
keeping OA fixed. P is a point on OB and PQ is perpendicular on OA. Therefore, OQ is base, PQ is perpendicular and OP is the hypotenuse of ![]() OPQ.
OPQ.
sin![]() =
= ![]() =
= ![]() , cos
, cos![]() =
= ![]() =
= ![]() , tan
, tan![]() =
= ![]() =
= ![]() ,
,
cosec![]() =
= ![]() =
= ![]() , sec
, sec![]() =
= ![]() =
= ![]() , cot
, cot![]() =
= ![]() =
= ![]() .
.
Therefore, sin![]()
![]() cosec
cosec![]() = 1,
= 1, ![]() = 1,
= 1, ![]() = 1
= 1
PROVE :
(i) ![]() +
+ ![]() = 1
= 1
Using Pythagoras’s theorem in ![]() OPQ we get,
OPQ we get, ![]() +
+ ![]() =
= ![]()
Or, ![]() +
+ ![]() = 1
= 1
Or, ![]() +
+ ![]() = 1
= 1
![]()
![]() +
+ ![]() = 1
= 1
(ii) ![]() –
– ![]() = 1
= 1
Using Pythagoras’s theorem in ![]() OPQ we get,
OPQ we get, ![]() +
+ ![]() =
= ![]()
Or, ![]() –
– ![]() =
= ![]()
Or, ![]() –
– ![]() = 1
= 1
Or, ![]() –
– ![]() = 1
= 1
![]()
![]() –
– ![]() = 1.
= 1.
(iii) ![]() –
– ![]() = 1
= 1
Using Pythagoras’s theorem in OPQ we get, PQ2 + OQ2 = OP2
Or, OP2 – PQ2 = OQ2
Or, ![]() = 1
= 1
Or, ![]() = 1
= 1
![]() sec2
sec2![]() – tan2
– tan2![]() = 1
= 1
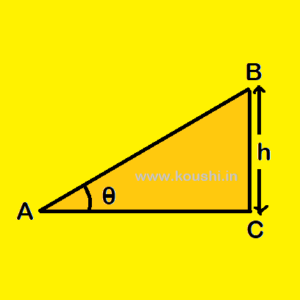
APPLICATION IN PHYSICS:
(i) An inclined plane AB of inclination ![]() is placed on ground at a height h. What is the length of AB?
is placed on ground at a height h. What is the length of AB?
Height of inclined plane BC = h. From ![]() ABC,
ABC, ![]() = sin
= sin![]()
Or, ![]() = sin
= sin![]()
![]() AB =
AB = ![]() = hcosec
= hcosec![]() .
.
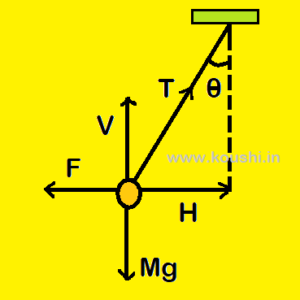
(ii) A bob of mass m is suspended freely from the celling by a string. Now a horizontal force F is applied on the bob and the string creates angle ![]() with vertical. What is the tension acts on the string if the bob is at rest?
with vertical. What is the tension acts on the string if the bob is at rest?
There are horizontal (H) and vertical (V) component of tension acts on the bob.
From diagram ![]() =
= ![]() so H = T
so H = T![]() and
and ![]() =
= ![]() so, V = T
so, V = T![]() .
.
As the bob is at rest then, F = T![]() and Mg = T
and Mg = T![]()
Now squaring and adding these two equations we get, ![]() +
+ ![]() =
= ![]() (
(![]() +
+ ![]() )
)
Or, ![]() =
= ![]() +
+ ![]()
![]() T =
T = ![]() .
.
TRIGONOMETRICAL RATIO OF SOME STANDARD ANGLES:
|
|
|
|
| |
sin | 0 | 1 | |||
cos | 1 | 0 | |||
tan | 0 | 1 | |||
cosec | 2 | 1 | |||
sec | 1 | 2 | |||
cot | 1 | 0 |
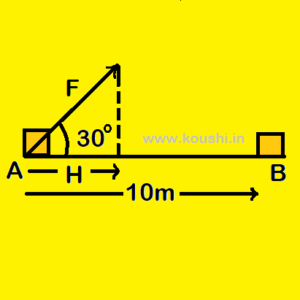
APPLICATION IN PHYSICS:
A block is moved point A to B (AB = 10m) by applying a force F = 10 N at an angle ![]() with AB. What is the work done required?
with AB. What is the work done required?
Work (W) = force (F) ![]() displacement.
displacement.
The component of force along AB is H and ![]() = cos
= cos![]()
Therefore, H = Fcos![]() = 10cos
= 10cos ![]() =
= ![]() = 5
= 5![]()
![]() W = 5
W = 5 ![]()
![]() 10 = 50
10 = 50![]() J.
J.
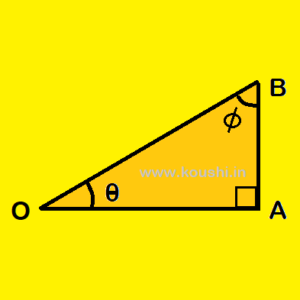
TRIGONOMETRICAL RATIO OF COMPLEMENTARY ANGLE:
If the sum of two angles is ![]() , then those two angles are called complementary angles. In figure
, then those two angles are called complementary angles. In figure ![]() OAB is a right-angled triangle.
OAB is a right-angled triangle. ![]() AOB =
AOB = ![]() and
and ![]() OBA =
OBA = ![]() and
and ![]() +
+ ![]() =
= ![]() and
and ![]() = (
= (![]() –
– ![]() ).
).
So, ![]() and
and ![]() are the complementary angles. From ,
are the complementary angles. From , ![]() OAB, sin
OAB, sin![]() =
= ![]() and cos
and cos![]() =
= ![]() . Therefore, sin
. Therefore, sin![]() = cos
= cos![]() = cos(
= cos(![]() –
– ![]() ). Similarly,
). Similarly,
| sin( | sec( |
| tan( | cot( |
| cosec( |
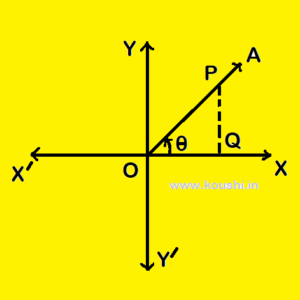
TRIGONOMETRICAL RATIO OF ASSOCIATED ANGLE:
Let us consider, XOX/ and ![]() are two mutually perpendicular axis where O is the origin. OA is a straight line which rotates about O in anticlockwise direction and creates an angle
are two mutually perpendicular axis where O is the origin. OA is a straight line which rotates about O in anticlockwise direction and creates an angle ![]() (acute angle). P is a point on OA and PQ is perpendicular on OX axis. From diagram OP, OQ and PQ are positive.
(acute angle). P is a point on OA and PQ is perpendicular on OX axis. From diagram OP, OQ and PQ are positive.
So, sin![]() =
= ![]() is positive, cos
is positive, cos![]() =
= ![]() is positive and tan
is positive and tan![]() =
= ![]() is positive. Similarly , cosec
is positive. Similarly , cosec![]() , sec
, sec![]() and cot
and cot![]() also positive.
also positive.
Therefore in 1st quadrant all trigonometrical ratio are positive.
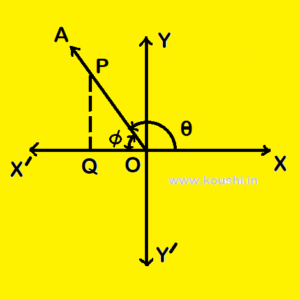
When OA is in 2nd quadrant then from diagram OP and PQ are positive but OQ is negative and ![]() +
+ ![]() =
= ![]() . So, sin
. So, sin![]() =
= ![]() is positive, cos
is positive, cos![]() =
= ![]() is negative and tan
is negative and tan![]() =
= ![]() is negative. Similarly cosec
is negative. Similarly cosec![]() is positive but sec
is positive but sec![]() and cot
and cot![]() are negative.
are negative.
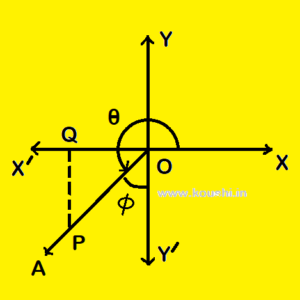
When OA is in 3rd quadrant then from diagram OP is positive but OQ and PQ are negative and ![]() +
+ ![]() =
= ![]() .
.
So, sin![]() =
= ![]() is negative, cos
is negative, cos![]() =
= ![]() is negative and tan
is negative and tan![]() =
= ![]() is positive. Similarly cosec
is positive. Similarly cosec![]() and sec
and sec![]() are negative but cot
are negative but cot![]() is positive.
is positive.
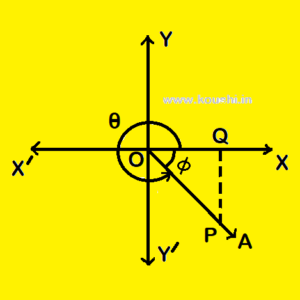
When OA is in 4th quadrant then from diagram OP and OQ are positive but PQ is negative and ![]() +
+ ![]() =
= ![]() .
.
So, sin![]() =
= ![]() is negative, cos
is negative, cos![]() =
= ![]() is positive and
is positive and
tan![]() =
= ![]() is negative.
is negative.
Similarly cosec![]() and cot
and cot![]() are negative but sec
are negative but sec![]() is positive.
is positive.
If ![]() is positive acute angle associated with the angle (n
is positive acute angle associated with the angle (n ![]()
![]()
![]()
![]() ) [where n is any positive integer (1, 2, 3, —–)], then to find the value of any trigonometrical ratio of this angle at first identify the quadrant in which the angle (n
) [where n is any positive integer (1, 2, 3, —–)], then to find the value of any trigonometrical ratio of this angle at first identify the quadrant in which the angle (n ![]()
![]()
![]()
![]() ) is located and use positive or negative sign with respect to the quadrant.
) is located and use positive or negative sign with respect to the quadrant.
When n is even | When n is odd |
| sin(n | sin(n |
| cos(n | cos(n |
| tan(n | tan(n |
| cosec(n | cosec(n |
| sec(n | sec(n |
| cot(n | cot(n |
EXAMPLE:
sin ![]() = sin(4
= sin(4 ![]()
![]() –
– ![]() ) = – sin
) = – sin ![]() = –
= – ![]() .
.
sin ![]() = sin(3
= sin(3 ![]()
![]() +
+ ![]() ) = – cos
) = – cos ![]() = –
= – ![]() .
.
cos ![]() = cos(4
= cos(4 ![]()
![]() +
+ ![]() ) = + cos
) = + cos ![]() = +
= + ![]() .
.
TRIGONOMETRICAL RATIO WHEN ANGLE IS VERY SMALL:
When ![]() is very small (less than
is very small (less than ![]() ) then sin
) then sin ![]() =
= ![]() , cos
, cos ![]() = 1 and tan
= 1 and tan ![]() =
= ![]() . For example,
. For example, ![]() =
= ![]() = 0.017453 and
= 0.017453 and
sin ![]() = 0.017452.
= 0.017452.
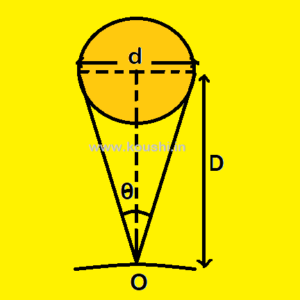
PARALLAX METHOD:
If you hold a pen in front of your eye and look the tip of the pen by closing the right eye and then the left eye keeping right eye open, then you observe that the position of the tip of the pen changes. This relative shift of the tip of the pen with respect to background is called parallax. The distance between two points of observations (the distance between your eyes) is called the basis. The angle subtended by basis at the object is called parallactic angle.
If a planet of diameter d is at a distance D (D ![]() d) and
d) and ![]() is the parallactic angle, then
is the parallactic angle, then ![]() is very small. From diagram we can write, tan
is very small. From diagram we can write, tan![]() =
= ![]() or,
or, ![]() =
= ![]() .
.
EXAMPLE: The distance between a star and earth is ![]() m. If the angular diameter of the planet is 1500// then find the diameter of the planet?
m. If the angular diameter of the planet is 1500// then find the diameter of the planet?
![]() = 1500// =
= 1500// = ![]() rad
rad
Distance between a star and earth is D = ![]() m.
m.
Diameter of the planet (d) = D![]() =
= ![]() =
= ![]() m.
m.
SOME IMPORTANT FORMULA:
The area of a circle with radius r is ![]() and circumference is 2
and circumference is 2![]() .
.
The surface area of a sphere with radius r is ![]() and volume is
and volume is ![]() .
.
The surface area of a solid cylinder with radius r and length l is 2![]() (r + l) and volume is
(r + l) and volume is ![]() .
.