Mirror formula:
If an object is at a distance u from the pole of a mirror of focal length f, then image distance is v. The Mirror formula is 
.
The derivation of mirror formula is given in the blog ‘Reflection class – XII‘. To get the information click the givenĀ button.
Graph:
The mirror formula isĀ .
Let us consider 
Ā = y, 
Ā = x and 
Ā = c
Then y + x = c
Or, y = – x + c
This is equation of straight line.
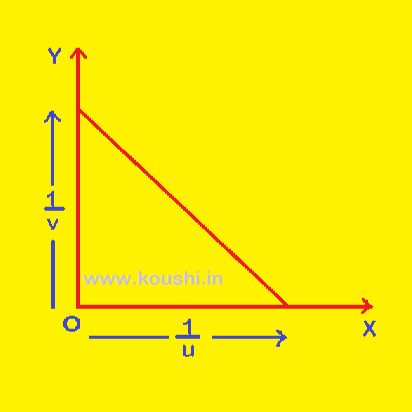
More information of graph is given in the blog ‘Reflection class – XII‘. To get the information click the givenĀ button.
Magnification power: The magnification is the ratio of the size (or height) of the image to the size (or height) of the object.
m = – 
= 
. Where h1Ā is the height of object and h2 is the height of image. For real image h2 is āve, and m is āve, for virtual image h2 is +ve and m is +ve.
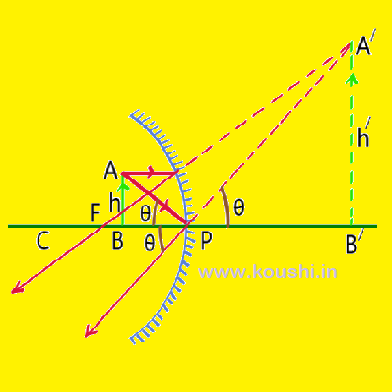
Magniļ¬cation in concave mirror (real image): Let us consider AB is an object of height h and after reflection A/B/ is the real image of the object of height h/. From figure 
ABP and A/B/P are similar. So, 
= 
Or, 
= 
Magniļ¬cation m = 
Ā = – .
Magniļ¬cation in concave mirror (virtual image): Let us consider AB is an object of height h and after reflection A/B/ is the virtual image of the object of height h/. From figure ABP and A/B/P are similar. So, =
Or, = 
Magniļ¬cation m = Ā = – .
Magnification in terms of object distance, image distance and focal length:
Let us consider an object of height ho is placed at a distance u from the pole of aĀ concave mirror of focal length f. Image is formed at a distance v from the pole of the mirror. The height of image is hi.
The mirror formula is 
Or, 
Or, 
Or, 
[Magniļ¬cation m = 
]
Or, 
Ā m = 
.
The mirror formula isĀ
Or, 
Or, 
Ā ā 1
Or, – m = 
Ā [Magniļ¬cation m = – 
]
Ā m = 
.
Newton’s equation: For a concave mirror the product of the distance between object and focus and distance between image and focus is equal to the focal length of that mirror.
The derivation of Newton’s equation is given in the blog ‘Reflection class – XII‘. To get the information click the givenĀ button.
Some numericals based on mirror formula are given below.
Example: 1. A concave mirror has a focal length of 10 cm. Calculate the image distance when an object is placed at a distance of 15 cm from the mirror.
Object distance u = -15 cm. Focal length of f = – 10 cm.
From mirror formula we get,Ā
Or, 
Or, 
Ā v = – 30 cm.
2. The focal length of a convex mirror is 30 cm and the size of the object is twice the size of the image. What is the image distance?
Focal length of the mirror f = + 30 cm. Convex mirror produces virtual image, so magnification m = – 
Ā = 
.
Here object distance u = – x
So, – 
=
Image distance v = 
Using mirror formula we get,
Or, 
Or, 
Ā x = 30
Image distance v = 
Ā = 15 cm.
3. The image of a point object placed at 10 cm from a concave mirror, is formed at a distance of 20 cm from the mirror. If the object is moved towards the mirror by 0.2 cm then what is the displacement of image?
Focal length of the mirror is f.
Object distance u = – 10 cm
Image distance v = – 20 cm
Using mirror formula we get,
Or, – Ā 
Or, 
Now object distance u = – 9.8 cm
Using mirror formula we get, 
Or, 
Or, 
Ā v = – 
Ā = 20.85 cm. Hence image will move another 0.85 cm away from the mirror.
4. A concave mirror of focal length 15 cm, forms an image having thrice of the linear dimensions of the object. If the image is virtual, then calculate the position of the object.
Let us consider the object distance is u = -x. Focal length f = – 15 cm.
Magnification m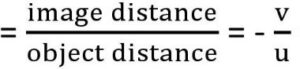Ā 
= 3
Or, – = 3
Or, v = 3xĀ Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā
Using mirror formula,
Or, – 
(putting the values)
xĀ = 
= 10 cm.
5. An object 4.0 cm in length is placed at a distance of 20 cm in front of a convex mirror of radius of curvature 30 cm. What is the position and size of the image?
For convex mirror, h0 = + 4cm, u = – 20 cm, f = 
= + 15 cm
Using mirror formula we get, Ā
Or, 
v = 
= + 8.57 cm
magnification m = 
= –
or, 
= – 
Ā hi = – 
= 1.714 cm.
6. Where an object should be placed in front of a concave mirror of focal length f, so that the image can be of the same size as that of the object?
As the size of image = size of object, therefore the image is real [in concave mirror virtual image is greater in size than that of object]. Let us consider u = – x.
Magnification m = -1Ā Ā
Or, – 1 = –
Or, – 1 = – 
Ā v = -x
Using the mirror formula we get,
Or, 
[focal length of concave mirror is negative]
Ā x = 2f
The object should be placed at 2F or at the centre of curvature of the mirror.
7. An object is kept in front of a concave mirror of focal length 20 cm. The image formed is 3 times the size of object. Calculate the possible distance of object from the mirror.
As the size of image is three times of size of object then magnification m = 3
If the image formed here is real then, -3 = – 
Ā or, v = 3u
Object distance u = -x
Image distance v = -3x
Focal length f = – 20 cm
Using the mirror formula we get,
Or, 
Or, 
Ā x = 
Ā = 26.6 cm.
If the image is formed here is virtual then, 3 = – Ā or, v = – 3u
Object distance u = -x
Image distance v = 3x
Focal length f = – 20 cm
Using the mirror formula we get,
Or, 
Or, 
Ā x = 
Ā = 13.3 cm.
The possible distance of object from the pole of the mirror are respectively – 26.6 cm and -13.3 cm.
More advanced level concepts are given in the blog ‘Reflection Class – XII‘. To get those information click the button given.
Paraxial rays, marginal rays: Those rays which incident on the spherical mirror near to the principle axis of the mirror are called paraxial ray. Those rays incident on the mirror just closer to the edge of the mirror is called marginal ray.Ā
The focal length of a spherical mirror due to marginal ray are less than that of paraxial ray.
More information of Paraxial rays, marginal rays are given in the blog ‘Reflection Class – XII‘.
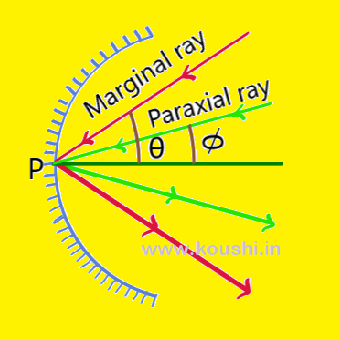
To get those information click the button given.
Click the button to goĀ to the previous part of this chapter.