Refraction through plane surface:
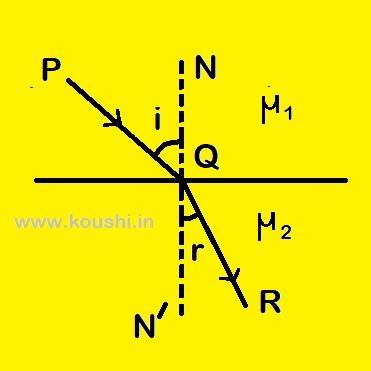
Laws of refraction: 1st law – The incident ray, the refracted ray, and the normal to the interface at the point of incidence, all lie on the same plane, called the plane of incidence.
2nd law – The ratio of the sine of angle of incidence (i) to the sine of angle of refraction (r) is constant for any two given medium and one colour of light. (Snell’s law) so, 
= constant.
Or,  = 1µ2 = 
. Where µ1 is the absolute refractive index of medium 1 in which incidence ray travels and µ2 is the absolute refractive index of medium 2 in which refracted ray travels.
Absolute refractive index: Absolute refractive index of a medium is defined as the ratio of speed of light in vacuum or air (c) to the speed of light in medium (v). So, µ = 
.
Relative refractive index: If medium 1 has refractive index µ1 and medium 2 has refractive index µ2 then, relative refractive index of medium 2 with respect to medium 1 is 1µ2 = .
Optical density of a medium: Let us consider the refractive index of medium 1 and medium 2 are respectively 
 and 
. If  > then the medium 1 is optically denser with respect to medium 2 or medium 2 is optically rarer with respect to medium 1. If any medium is optically denser then we cannot say that the specific gravity or density of that medium is also high. The specific gravity of turpentine oil is 0.87 and that of water is 1 but refractive index of turpentine oil is 1.47 and that of water is 1.33.Â
Relation between refractive index of medium and wavelength of light: Let us consider the velocity of monochromatic ray of light in vacuum and in a medium are respectively c and v. The refractive index of medium is 
= 
.
The frequency of light is n and wavelength of it in vacuum and in medium are respectively 
 and 
. Therefore, Â = 
 = 
.
Example: 1. Refractive index of glass is 1.5 and refractive index of water is 1.33. If the velocity of light in glass is 2 
108 ms-1, then what is the velocity of light in water?
Refractive index of glass with respect to air is 
= 
Or, 
= 
Or, c = 
vg  —– (i)
Similarly if 
 and Vw are the absolute refractive index and velocity of light in water, then c = vw —– (ii)
From equation (i) and (ii) we get, Â = vg = vw
Or, 1.5 2 108 = 1.33 vw
 vw = 
 = 2.26 108 ms-1.
2. How much time will light take to pass through the glass slab of thickness d. The absolute refractive index of glass is .
The absolute refractive index of glass is = Â =
Or, vg = 
If t is the time taken to travel the distance d by light then, vg = 
Or, 
=
  t = 
.
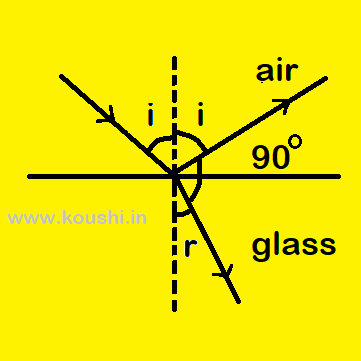
3. A ray of light is incident on glass slab from air in such a way that the angle between the reflected and refracted ray is 900. What is the relation between the angle of incidence and the refractive index of glass?
Let us consider the angle of incidence and angle of reflection are i and angle of refraction is r. As the angle between reflected and refracted ray is 900 then, i + r + 900 = 1800
Or, r = 900 – i
If is the refractive index of glass with respect to air then using Snell’s law we get, Â =
Or, = 
  = 
 = tani.
Click the button to go the next part of this chapter.