Refraction Class - XII Part - 2

Refraction through a glass slab: Let us consider a rectangular glass slab of refractive index µ and thickness t placed in air. A ray of light AB incident at B with angle of incidence i. After refraction, the ray of light bends towards the normal and goes along BC such that r is the angle of refraction.

Using Snell’s law at point B we get, = _aµ_g —–(1)

At point C, the ray of light again suffers refraction and emerges out of the glass into air along CD. For refraction at C, r is the angle of incidence and i^/ is the angle of refraction. Using Snell’s law at point C we get, = _gµ_a ——(2)

From equation (1) and equation (2) we get, = = _aµ_g _gµ_a

Or, = 1 [as _aµ_g = ]

Or, sin i = sin i^/

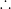i = i^/

So, the ray of light incident on a parallel glass slab emerge out parallel to the incident ray.

Lateral shift: The perpendicular distance between the direction of incident ray and the emergent ray is known as lateral shift. Using Snell’s law at point B we get, = _aµ_g = µ (absolute refractive index of glass) ——-(i)

And cos r = = 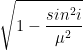———(ii)

From figure CE is the lateral shift. From BCE, CE = BCsin(i – r) ——(iii)

From BN₂C, = cosr

Or, = cosr

Or, BC = ——-(iv)

From equation (iii) and equation (iv) we get, lateral shift CE =

Or, CE = [sinicosr – cosisinr]

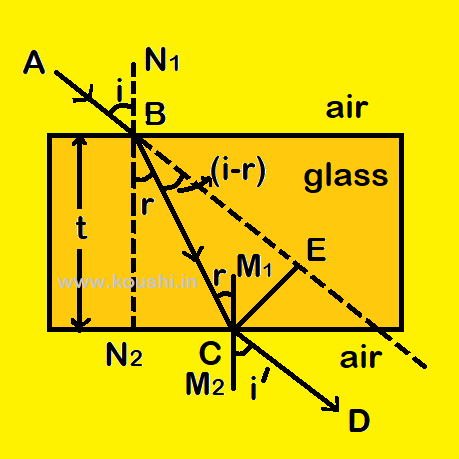
Or, CE = t[sini – ]

Or, CE = t[sini – 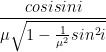] [using equation (ii)]

Or, CE = tsini[1 – ].

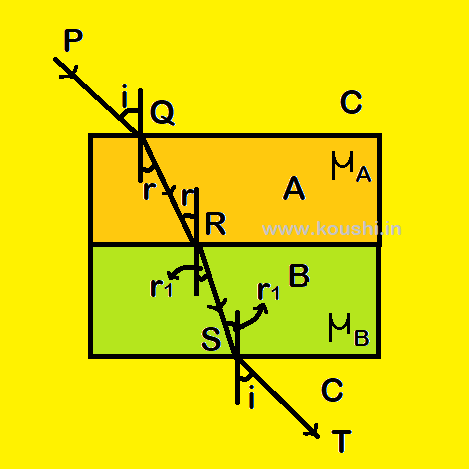
Refraction through compound slabs: Let us consider two parallel slabs (slab A and slab B) of absolute refractive index µ_A and µ_B respectively are placed one over another as shown in figure. C is the medium above and below the slabs with absolute refractive index µ_C. Let PQ is the incident ray on slab A from medium C and ST is the emergent ray from slab B in medium C. As the slabs are parallel and incident and emergent medium are same then the angle of incidence and angle of emergence are same (say i).

Using Snell’s law at point Q when ray PQ passes from medium C to medium A we get, = _Cµ_A——-(i)

Using Snell’s law at point R when ray QR passes from medium A to medium B we get, = _Aµ_B——-(ii)

Using Snell’s law at point S when ray RS passes from medium B to medium C we get, = _Bµ_C——-(iii)

Multiplying equations (i), (ii) and (iii) we get,

= (_Cµ_A) ( _Aµ_B) (_Bµ_C)

Or, (_Cµ_A) ( _Aµ_B) (_Bµ_C) = 1

Or, _Aµ_B = = ——(iv)

If medium C is air then _Cµ_A = µ_A and _Cµ_B = µ_B then from equation (iv) we get, _Aµ_B = .

Example: Refractive index of water with respect to air is 1.33, refractive index of oil with respect to water is 1.35 and that of glass with respect to oil is 0.65. What is the refractive index of glass with respect to air?

Refractive index of water with respect to air is = 1.33

Refractive index of oil with respect to water is = 1.35

Refractive index of glass with respect to oil is = 0.65

We know that = 1

Or, = =

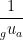= 1.331.350.65 = 1.167.

Relation between refractive index with real depth of an object (when object is placed in a denser medium): Let us consider a point object is placed at point O in medium 1 of refractive index µ. Ray of light travels from OA and refracts in air at point A with angle of incidence i and angle of refraction r. Another ray ODE passes normally in air without deviation. When point O is observed from air, refracted ray AB moves away from normal, so it shifts at point C as shown in figure. Therefore, DO is real depth and DC is the apparent depth of the point object. As the aperture of eye is small then the angle subtended at eye by the rays are very small.

Then sini = tani = and sinr =tanr = .

Using Snell’s law at point A we get, = ₁µ_a = =

Or, =

Refractive index = .

Relation between refractive index of a medium with apparent and real depth of an object (when object is placed in a rarer medium): Let us consider an object O is placed in a medium of refractive index . The object is observed from a denser medium of refractive index . A ray of light OAB passes perpendicularly on the interface of two medium without any deviation. Another ray of light incident at point C at an angle i and refracted along the path CD at an angle r. When the ray AB and CD come to an observer who is in denser medium, a virtual image is formed at point P.

Therefore in this case the image appears to move far away from object. As points A and C are very close to each other then all angles are very small. Therefore, sin = tan = .

Using Snell’s law at point C we get, ₁µ₂ =

Or, =

Or, = =

If medium 1 is air then, = 1 and =

Therefore, =

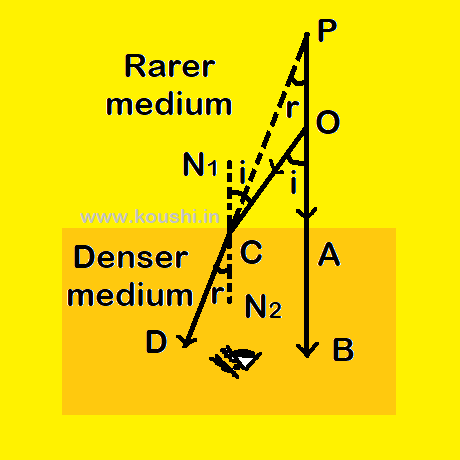
Refractive index of denser medium with respect to rarer medium = .

A vessel is filled with two immiscible liquid 1 and 2 of refractive index and with depth d₁ and d₂ respectively. There is a point at the bottom of the vessel. Find the apparent depth of the point when viewed normally from air. The image of point O is formed at point D due to refraction at point A on the interface of liquid 1 and 2. When it is viewed from air, point D is sifted at point F. As points B and G are very closed to each other then all angles are very small. Therefore, sin = tan = .

Using Snell’s law at point A we get, = ₁µ₂ =

Or, =

Or, = ——– (i)

For the refraction of light at point B, GD is considered as real depth and GF is the apparent depth.

Using Snell’s law at point B we get, = ₂µ_a =

Or, = [Refractive index of air is = 1]

Or, =

Or, GF = = = + = + [Using equation (i)]

Apparent depth of point O = + .

Example: 1. There is a black spot at the bottom of a rectangular glass slab of thickness d and refractive index . When the spot is viewed perpendicularly from air, find the shifted distance of the spot.

Real depth of the black spot from the upper surface of the glass slab is d.

The apparent depth of the black spot from the upper surface of the glass slab is x.

Therefore, refractive index of glass = =

Or, x =

The apparent displacement of the spot is y = (d – x) = d – = d(1- ).

2. A point source is placed at a distance of 3d from the pole of a concave mirror and its image is formed at a distance of 1.5d from the mirror. A glass slab of thickness d is placed between the point source and the mirror such that the parallel face of the glass slab remains perpendicular to the principal axis of the mirror. If the refractive index of glass slab is , then calculate the position of the image.

Let us consider O is the position of the object and I is a position of image after reflection through the concave mirror when the glass slab is absent.

Therefore, object distance is PO = u = – 3d. Image distance is PI = v = – 1.5d. Focal length of the mirror is – f. Using mirror formula we get,

Or,

Or, =

f = d

When the glass slab is placed between the object and concave mirror, apparent displacement of the point source will take place towards the mirror. Now the rays coming from point O^/ and after reflection from mirror image is formed at point I^/.

Apparent displacement of point O is OO^/ = d(1- ).

Now object distance is PO^/ = PO – OO^/ = 3d – d(1- ) = d(2 + )

Focal length of the mirror is f = – d

The final image distance = v

Using mirror formula we get,

Or, – = –