Relative velocity: Theory

By koushiadmin
(0) comments
June 28, 2025

Relative velocity: Theory

RELATIVE VELOCITY THEORY AND CONCEPTS

THEORY: Relative velocity: Let us consider and are the velocity of two particles A and B creates angleθ. The velocity of A with respect to B is = –. The angle between and – is (180- θ) and is the resultant of and – .

The magnitudes of is V_AB² = V_A² +V_B²+ 2V_AV_{B cos(180-θ)}

Or, V_AB² = V_A² +V_B²+ 2V_AV_{B cosθ}.

If creates angle φ with then, φ =

Or, tanφ = .

CONCEPTS ON RELATIVE VELOCITY IN ONE DIMENSION:

Two towns A and B are connected by a regular bus service with a bus leaving in either direction in every T minutes. A man cycling with speed of u in the direction from A to B notices that a bus goes pass him every t₁ minutes in the direction of his motion, and every t₂ minutes (t_1>t₂) in the opposite direction of his motion. What is the period T of the bus service and with what speed (assume constant) do the busses ply on the road?

Let us consider speed of each bus is v and the distance between the nearest two busses plying on either side is vT.

For bus going from town A to B:

Speed of bus with respect to cyclist is (v-u). As the cyclist notices that a bus goes pass him every t₁ minutes in the direction of his motion, then the separation between the busses is (v-u)t₁. So, vT = (v-u)t₁ —- (i)

For bus going from town B to A:

Speed of bus with respect to cyclist is (v+u). As the cyclist notices that a bus goes pass him every t₂ minutes in the opposite direction of his motion, then the separation between the busses is (v+u)t₂. So, vT = (v+u)t₂—- (ii)

From equations (i) and (ii) (v-u)t₁ = (v+u)t₂

Or, v = .

Using equation (i) vT = (v-u)t₁

∴T = .

A polish van moving with speed u on a highway fires a bullet at a thief’s car which is moving away with speed v in the same direction. If the muzzle speed of the bullet is w, with what speed does the bullet hit the thief’s car?

Muzzle speed is the speed of bullet with respect to the van. Speed of van or velocity of thief’s car are measured with respect to ground.

So, velocity of bullet with respect to van = velocity of bullet with respect to ground – velocity of van with respect to ground

W = velocity of bullet with respect to ground – u

Or, velocity of bullet with respect to ground = w + u.

Now, velocity of bullet with respect to thief’s car = velocity of bullet with respect to ground – velocity of thief’s car with respect to ground

So, velocity of bullet with respect to thief’s car = w + u – v.

On a two lane road, car A is moving with speed u. Two cars B and C approach car A in opposite direction with speed 2u. At a certain instant, when the distance AB = AC = d, driver of car B, decides to overtake A before C does. What minimum acceleration of car B is required to avoid accident?

At the instant when driver of car B, decides to overtake A the velocities of car A, B and C are respectively V_A = u, V_B = 2u and V_C = -2u [ -ve due to opposite direction].

Velocity of car B with respect to car A is V_BA = V_B – V_A = 2u – u = u.

Velocity of car C with respect to car A is V_CA = V_C – V_A = -2u – u = -3u.

Time required by C to cross A is t = = .

To avoid accident, car B must overtake car A in this time. Therefore, d = V_BAt + at²

Or, d = u() + a()²

So, a = .

CONCEPTS ON RELATIVE VELOCITY IN ONE DIMENSION:

Two trains, each having a speed of u kmh^-1 are headed towards each other on the same straight track. A bird can fly with speed 2u kmh^-1 from one train and heads directly to the other train, when they are 2u km apart. On reaching the other train, it flies directly back to the first and so on. (i) How much trips can the bird make from one train to the other before they collide? (ii) What is the total distance travelled by the bird?

The velocity of one train relative to the other is u – (-u) = 2u. The collision time is 2u = 2ut (s = vt) or, t = 1h. So bird moves for 1h. Now the velocity of bird with respect to train towards which it is moving will be 2u – (-u) = 3u kmh^-1.

So, the time taken by bird for 1^st trip, t₁ = () = h.

In this time the trains have moved towards each other 2u× = km, so the remaining distance = 2u – =

So, the time taken by bird for 2^nd trip t₂ =× = .

Similarly, time taken by the bird for nth trip is t_n = .

Therefore, + + —– + = 1

Or, []

Or,1- = 1

Or, = ∞

∴ n = ∞.

So, the bird makes infinite trips.

Distance travelled by bird for 1^st trip is s₁ = 2ut₁ = 2u ×= km.

Distance travelled by bird for2^nd trip is s₂ = 2ut₂ = 2u× = km.

Distance travelled by bird for n^th trip is s_n = 2ut_n = 2u× = km.

So, total distance travelled by bird forinfinite trip is s = + + + ——∞

= [1 + + + ——–∞]

= [] = 2u.

Man is moving on inclined surface with constant speed: A man is coming down through an inclined surface of inclination 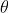with speed u. He has to keep his umbrella vertical to protect him and the velocity of rain with respect to man is v. Find the actual velocity of rain.

The velocity of man with respect to ground is = ucos – usin.

The velocity of rain with respect to man is = – v.

We know that = – so, = + = – v + ucos – usin = ucos – (usin +v)

Therefore, actual velocity of rain is and angle with vertical is = ()

Man is moving on horizontal surface with constant acceleration: Rain is falling vertically with speed u. A man starting from rest moving with constant acceleration a. Find the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain falls parallel to the axis of umbrella.

The velocity of man with respect to ground at any instant of time t is = at [v = at].

The velocity of rain with respect to ground is = u.

The velocity of rain with respect to man is = – .

At any instant rain appears to the man at an angle , so,tan = .

We have to find the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain falls parallel to the axis of umbrella. Therefore, we need .