Work Energy Power
Work: Work is said to be done when a force is applied on a body and the body is displaced through a certain distance in the direction of the applied force.
If F is the force is applied on a body at an angle θ with displacement S, then work done on the body is W = FcosθS = 
.
Unit: SI unit of work is joule (J) = 1newton × 1meter
C.G.S. unit of work is erg = 1dyne × 1centimeter
1J = 105dyne102cm = 107erg.
Dimension of work [W] = [F][S] = [MLT-2][L] = [ML2 T-2].
Positive work: If force (or its component) and displacement are in same direction (00<θ <900) then the work done is positive. Example: A body is falling vertically under gravity.
Negative work: If force (or its component) and displacement are in opposite direction
(900<θ <1800) then the work done is negative. Example: A body is projected vertically upward against gravity.
Zero work: If force and displacement are in perpendicular direction (θ = 900) then the work done is zero and the force is called no work force. Example: A man holds a suitcase in his hand moves in horizontal road.
If the displacement of the body or applied force on it is zero then also the work done is zero.
Work done on a body is different depending on the frame of reference:Let us consider observer A and B are fixed with two reference frame (inertial) X and Y respectively. A force F is applied on a block C. Let us consider 
and 
are the work done with respect to observe A and B respectively whenever F force is acting on the block.
If Δ
and Δ
are the displacement observed by observer A and B respectively for any interval of time, then the corresponding work done is given by = .Δ
and = .Δ 
.
Therefore, if same force is applied on a body then work done are different relative to different frame of reference.
Example: A block of mass M is placed on an incline plane of inclination 
. It is moved upward direction from A to B by a constant force F actingparallel to the incline plane. Calculate the work done by the gravitational force, external force F and also calculate the net work done.
R is the normal reaction applied by the inclined surface on the block.
If we resolute the weight of the block mg, R = Mgcos.
Here R and Mgcos are perpendicular to the displacement of the block AB (= s).So, they does not perform any work.
The work done due to gravitational force to move the block from A to B is Wgravitational = Mgsinscos 1800 = – Mgssin.
The work done by the external force F to move the block from A to B is Wexternal = Fscos00 = Fs.
The network done on the block isWnet = (F – Mgsin)s.
Work done by a variable force:If either the magnitude or direction or both the magnitude and direction of the applied force change, then we can say the force is variable.To calculate the work done by the variable force we have to consider the work done for an infinitesimal displacement 
i.e. dw = . .
The total work done by the variable force to move the body from A to B is
W = 
dw = 
. = Fds cos .
Example: 1. A force F = ax acts on a particle along positive x axis where a is a constant and x is the displacement of the particle at any instant. Calculate the work done to move the particle by the force along positive x axis from x1 to x2.
At any instant the position of the particle is x, therefore force acting on the particle is F = ax.
The work done to displace the particle for dx is dw =d
= Fdxcos00 = axdx.
Therefore, the total work done to displace the particle from x1to x2 is Wdw =
axdx = 
.
- Force F = at3 is applied on a body of mass M where a is constant and t is time. Calculate the work done by the force for 1st 2 second.
As the force is variable then the acceleration of the particle at any instant of time t is a = 
Or, a = 
Or, =
Or, dv = dt
Or, =∫dv = ∫dt
∴ v = 
this is the velocity of the body at instant of time t.
The work done at any instant of time t for the displacement dx of the body is dw = Fdx = F
dt
Or, dw = Fvdt
Or, dw = 
dt
The total work done on the body for 2 second is w = dw = 
dt
Or, w = 
Or, w = 
∴ w = 
.
- A uniform chain of mass M length L is held on a frictionless table with
th part of its length hanging from the edge of the table.Calculate the work done to pull the chain slowly on the table against gravity.
As the chain is uniform then mass per unit length of the chain is λ= 
.
The length of the hanging part of the chain is 
. We consider an elementary part of the chain of length dy at a distance y from the edge of the table.
Mass of that elementary part of chain dm =
The work done to pull the dm part up to a height y is dw = dmgy = 
.
Therefore, the work done to pull the hanging part of chain on the table is
w = ∫dw = 
= 
= 
= 
.
We can solve the numerical in alternate method: The mass of the hanging part of the chain is 
. The length of the hanging part of the chain is 
. As the mass is uniformly distributed, the centre of mass of the hanging part is at a distance of 
from the edge of the table.Therefore, the work done required to pull the length of the chain on the table is w = change in potential energy =( )g() = .
Work done by the pair of interactive force:The interacting forces like electrostatic force, gravitational force of attraction, spring force, friction etc. can perform work on a system.
Let us consider two particles A and Binteract with each other by a pair of action reaction forces and – respectively.
Also consider dxA and dxB are the elementary displacement of the particles A and B respectively.
Work done on particle A is dwA = FdxA
Work done on particle B is dwB = -FdxB
Total work done on the system for elementary displacement is dw = dwA + dwB = F(dxA-dxB) = FdxAB —– (i)
WheredxAB is the elementary displacement of particle A with respect to particle B.
- When there is no relative displacement between these particles, then dxAB = 0, so dw = 0 [using equation (i)]
The relative displacement is zero under constrain forces like tension on inextensible string.
- When two particles are moved by mutual attractive orrepulsive force like electrostatic force gravitational force, then there is a relative displacement. In such cases interaction force performs non zero work.
Work done by static friction: When static friction is acting between body and the surface, then there is no relative displacement between body and surface. Therefore, static friction doesn’t perform any work.
If a body is placed on a rough surface and force is applied on the body and we have to calculate the work done by the force, then at first calculate the value of limiting friction.If the value of limiting friction is greater than the applied force, it signifies that there is no relative displacement between body and the surface.Therefore, the work done by the force on the body is zero.
Example: A block of mass M is placed on a smooth surface and another block of mass m is placed on M. F force is applied on M for time t as shown in figure. We assume that frictional forceacts between two blocks and there is no relative displacement between them.Calculate work done by static friction on blocks. Calculate work done by the external force.
As there is no relative displacement between two blocks and the horizontal surface is smooth, then two blocks will move with same acceleration a =
.
The value of limiting friction fs = ma = 
.
As F force is applied on block M towards right, therefore static friction applied by m on M acts towards left.Similarly static friction applied by M on m is towards right.
The displacement of blocks for time t is s =
= 
The work done by static friction on M is WM = -fs.s = –
. [Displacement and friction is in opposite direction]
The work done by static friction on m is Wm = fs.s = . [Displacement and friction is in same direction]
Net work done by static friction is W = WM + Wm = -fs.s + fs.s = 0.
Work done by the external force is WF = Fs = .
Work done by kinetic friction:When a body slides over a rough surface then there is a relative displacement between the surface and the body and kinetic friction acts between the body and the surface. Therefore, kinetic friction performswork.
If fk is the kinetic friction acting on the body opposite to the displacement s,then work done by the friction on the body is W = – fks.
If the surface is fixed, then work done by the friction on the surface is zero.
Work done by the kinetic friction when a body is moved on a movable surface:Let us consider a block of mass m is placed on a plank of mass M as shown in figure.
Friction acts between the body and the plank. The surface on which the plank is placed is smooth.
Initially the block is moving with speed v relative to the plank and slide a distance x relative to the plank. fk is the kinetic friction acts on the block by plank towards left and the block moves a distance x1. The work done by the friction on block is WB = -fkx1.
Friction applied by block on plank is towards right and displacement of plank x2 is also towards right.Therefore the work done by the friction on plank is WP = fkx2.
The total work done by the frictional force is
W = WB + WP =-fkx1+ fkx2 = – fk(x1 – x2) = -fkx.
Example: A block of mass m is moved on a rough horizontal surface with constant speed by applying force at an angle 600 with vertical. The coefficient of friction between surface and block is . Find the work done to move the block for a distance s on the surface.
Let us consider F force is applied on the body. The horizontal component of applied force is Fsin600 = 
.
As the body is moved with constant speed then, horizontal component of applied force = frictional force
Or, =
R
Or, = (mg – Fcos600)
Or, = (mg –
)
Or, +
= mg
∴F = 
The work done to move the body for a distance s on the surface is w = horizontal component of applied force × distance travelled
w =
=
() = 
.
Work done is represented by the area under force versus displacement graph.
Example: The variation of applied force F with displacement x of a particle is given in the graph.Calculate the work done of the particle for thedisplacement of 5m.
The total work done of the particle consists of two parts.One is positive work done W1 and the other is negative work done W2.
W1 = area of the trapezium OABC = 
[2+4]2 = 6 J.
W2 = area of triangle CDE = × (-3) ×1 = – 1.5 J.
The total work done of the particle is W = W1 + W2 = 6 -1.5 = 4.5 J.
Conservative and non-conservative field: A force is said to be conservative if the work done by or against the force in moving a body depends only on the initial and final position of the body not the nature of the path. Gravitational force, electrostatic force between two stationary charges, spring force etc. are conservative force.
Gravitational force is a conservative force because if we move a particle of mass m against gravity for a height h then the potential energy is –mgh. It does not depend on path. It depends only the initial and final position of the particle.
Magnetic field is neither conservative nor non-conservative.
When electric field is produced by static charge, it is conservative.When electric field is produced by time varying magnetic field then it is non-conservative.
For conservative force, work done is path independent. Work done in a closed path is zero.For conservative force, work done is equal to change in potential energy.
A force is said to be non-conservative if the work done by or against the force in moving a body depends upon the initial and final position of the body and the nature of the path. Frictional force, viscous force etc. are non-conservative force.
For non-conservative force, work done depends on path.For a closed path work done is not zero. For non-conservative force work done is not equal to change in potential energy.
Kinetic energy: The energy possessed by a body by virtue of its motion is called kinetic energy.
Let us consider a body of mass m is initially at rest. It is applied by an external force F and the velocity of the body is v after travelling a distance s. The acceleration of the body is a = 
.
Then, v2 = 2as
Or, v2 = 
Or, Fs = 
Or, W = K.E. of the body.
Relation between kinetic energy and momentum of body: Let us consider a body of mass m is moving with velocity v, then the kinetic energy of the body is E = mv2 and the momentum of the body is P = mv.
Or, E = 
= 
Or, P = 
.
(1) If two bodies of same mass moving with kinetic energy E1 and E2 then the ratio of momentum P1: P2 = 
:
.
(2) If two bodies are moving with same kinetic energy but of different masses m1 and m2 then the ratio of momentum P1😛2 = 
:
.
(3) If two bodies of masses m1 and m2 are moving with kinetic energy E1 and E2 and momentum of two bodies remain same then, m1: m2 = E2:E1.
Kinetic energy due to explosion: Let us consider a body is initially at rest. Due to explosion the body is divided into two parts. One part of mass m is moving with speed u and the other part of mass M (M>m) is moving with speed v in opposite direction. The kinetic energy of masses m and M are Em and EM respectively.
Therefore, 
= 
= 
.
Using conservation of linear momentum, we get, mu = MV or, u = 
.
So, = 
= 
.
Therefore, kinetic energy is inversely proportional of mass. As M>m, so, Em> EM.
If the total kinetic energy is E, then E = Em + EM = 
+
Or, E = 
Or, E = 
Or, E = 
Or, E = 
Or, EM = 
Similarly, Em = 
.
.
Example: 1. A ball is moving with speed v and after striking by bat the ball is moved with speed 1.5v in opposite direction. Find the change in momentum of the ball if the change in kinetic energy is E.
Let us consider the mas of the ball is m. The change in kinetic energy is E = 
– = 
Or, m = 
.
Therefore, change in momentum of the ball = m[1.5v – (-v)] = 2.5mv = 
= 
.
- A body of mass m is initially at rest. F force is applied on it for time t. Find the kinetic energy of the body at time t.
The acceleration of the body is a =
. The speed of the body at time t becomes v = at =
.
The kinetic energy of the body at time t is E = = 
= 
Work energy theorem:Work done by all forces like conservative, non-conservative, external, internal acting on a particle is equal to the change in kinetic energy of it.
Therefore, according to work energy theorem we can say that the work done by the resultant force acting on the particle (which is equal to the sum of work done by individual forces) is equal to the change in kinetic energy of it.
If the total work done is positive then the kinetic energy will increase and if work done is negative then the kinetic energy will decrease.
Let us consider a body of mass m is moving with initially speed u. It is applied by an external force F and the velocity of the body is v after travelling a distance s. The acceleration of the body is a = .
Then v2 =u2 + 2as
Or, v2 – u2 =
Or, Fs = 
Or, W = change in K.E. of the body.
Work energy theorem for variable forces: The work done by a force on a body is equal to the change in kinetic energy of the body.
Let us consider a body of mass m is moving with initially speed v and the kinetic energy of the body is E = mv2
Differentiating both side with respect to time t, we get 
=
[mv2] = m2v
= mv = mva [acceleration a = ]
Or, = ma 
[as v= ]
Or, dE = Fdx = dw ——-(1)
When x = xi, KE = (KE)I and w =0 and when x = xf,, KE = (KE)f and w = W
Integrating both side of equation (1), we get,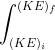 
dE = 
dw
Or,[(KE)f – (KE)i] = W
So, the work done by a force on a body is equal to the change in kinetic energy of the body.
Work energy theorem is also applicable for non-inertial frame of reference.At that case we have to consider the work done by the pseudo force also.
Example: 1. A plank of mass M is on a frictionless horizontal surface is applied by a constant force F.Another block of mass m is placed on the plank. There is no relative displacement between plank and block. We can consider the following conditions.
As there is no relative displacement between block and plank, both will move with same acceleration a = . The frictional force generates in between the surface of block and plank.The frictional force acting on block by plank is in forward direction and it is f = ma = 
.
Observed from ground (inertial frame of reference): As there is no relative displacement between block and plank, therefore block and plank move distance s and at that instant velocity is v.
The work done by the friction on the block is Wf = fs = 
.
From work energy theorem,Wf = K.E.f – K.E.i
Or, fs =
Or, =
∴ v = 
.
Observed from plank (non-inertial frame of reference): In this case pseudo force acting on the block which is equal to frictional force as there is no displacement of block with respect to plank.
Therefore, total work done W = Wf + WP = – = 0 [pseudo force is opposite to the displacement hence the work done due to pseudo force is negative]
From work energy theorem, W = change in K.E.
Or,
= 0
vr = 0 [vr is the velocity of block relative to plank].
- A body of mass m is slowly moved up through a curved surface from position A to B by a force F which is directed at each point along the tangent to the trajectory.Find the work done performed by this force if the height of point B is h and horizontal length of the base is L.The coefficient of friction is .
There are four forces acting on the body, (i) weight of the body (ii) normal reaction applied by the surface on body, (iii) frictional force (iv) applied force.
Using work energy theorem we get, the work done by all forces = change in kinetic energy
Therefore, Wmg + WN + Wfriction + WF = Δ K.E. ——— (i)
As gravitational force is conservative force, then – Wmg = Uf – Ui = mgh – 0
Or, Wmg = – mgh.
Normal reaction at all points is perpendicular to the displacement, then the work done by normal reaction is zero. So, WN = 0
Frictional force f =
The work done by the frictional force for the displacement ds is
dw = mgcos
ds = –mgdl
The work done by the frictional force to displace the body from point A to point B is W = ∫dw = 
– mgdl= – mgdl
From equation (i) we get,- mgh – mgdl + WF = 0
WF = mg(h + L )
Potential energy: The energy possesses by a body by virtue of its position or configuration (shape) is called potential energy. Potential energy is defined as the work done by a conservative force.Force always do positive work at the expense of its potential energy stored in the field.The loss of potential energy is equal to the total work done by the conservative forces.
Whenever the elongation or compression of a spring decreases, the spring force decreases it means that the work done by the spring is equal to the loss of its potential energy.
Example: A pendulum initially is at rest position at point A. If the bob is pulled slowly towards right at point B, find the change in gravitational potential energy of the pendulum as a function of x. The effective length of the pendulum is l and mass of the bob is m.
When the bob is at point B then the vertical height travel by the bob from initial point A is h.
If the string of the pendulum creates an angle with the vertical at point B, then
cos = 
= 
.
Initial potential energy of the bob at point A = 0
Final potential energy of the bob at point B = mgAC = mg(OA – OC)
= mgl(1- cos)
= mgl(1- ).
Change in potential energy of the bob is mgl(1- ).
Relation between conservative force with potential energy: Change in potential energy of a particle between two points in the conservative field is defined as the work done by the associated conservative force to displace the particle between those two points without any change in kinetic energy.
Let us consider two points A and B in a conservative field are separated by infinitesimal distance dr.A particle is moved in between two points byconservative force F. The potential energy at those points are respectively UA and UB.The work done required to move the particle from point A to point B isdW = Fdr. The change in potential energy is dU = UB – UA
Therefore, dU = – Fdr
Or, F = –
Or, ΔU = Uf – Ui = –
.
= – W
If we consider the reference point at infinity, then the potential energy at infinity is zero.
So,U = Uf –
= – 
= – W.
In Cartesian co-ordinate system the components of a force is in x,y,z axis can be given as the negative gradient of potential energy measured along the corresponding axis.
Therefore,
= –
, 
= – 
and 
= – 
So, = – ( + + )
Where is the partial differentiation of U with respect to x when y and z are constant.
is the partial differentiation of U with respect to y when x and z are constant.
is the partial differentiation of U with respect to z when x and y are constant.
Potential energy graph:The variation of potential energy with displacement is shown in graph. The force acting on the particle is defined as the negative gradient of potential energy (F = – 
) .
We can consider the following factors from the graph.
In the region from AB, the potential energy decreases with increase of x. Therefore, is negative and the direction of F is positive i.e. repulsive in nature.
In the region BC, the potential energy increases with increase of x. Therefore, is positive and the direction of F is negative i.e. attractive in nature.
At point B, C and D is zero therefore no force is acting at these points, hence the particle is in equilibrium at those points.
The potential energy of the particle changes with displacement is given in the graph. The stability of the particle is explained from the graph. Let usconsider some points on the graph.
Stable equilibrium:Let usconsider points 1 and 2 very close to point A.At point 1 potential energy decreases with increase of x. Therefore, 
<0 and force F1(= – ) is positive in direction.Similarly at point 2 potential energy increases with increase of x.Therefore,> 0 and force F2 (= – ) is negative in direction. The slope changes from negative to positive at point A when we move along positive x direction. The direction of force changes from positive to negative at point A.Therefore, it indicates that the force is always towards that point A. If the particle which is at point A is slightly displaced, it always returns to point A. Therefore, at point A the particle is in stable equilibrium.
The condition of stable equilibrium is = 0 and 
> 0.
Unstable equilibrium:Let us consider points 3 and 4 very close to point B.At point 3 potential energy increase with increase of x. Therefore, >0 and force F3 (= –) is negative in direction. Similarly at point 4 potential energy decreases with increase of x. Therefore,< 0 and force F4 (= – ) is positive in direction. The slope changes frompositive tonegative at point B when we move along positive x direction. The direction of force changes from negative to positive at point B. Therefore it indicates that the force is always away from point B. If the particle which is at point B is slightly displaced,it will never come to that point. Therefore, at point B the particle is in unstable equilibrium.
The condition of unstable equilibrium is = 0 and < 0.
Neutral equilibrium:Let us consider two points 5 and 6 very close to point C.At point C there is no change of potential energy with respect to x. Therefore, = 0 and the particle experience zero force when it is displacednear point C.At that condition we can say that particle is in neutral equilibrium.
Example: The potential energy of a particle in conservative force field is given by U = ax2 – bx, where a and b are the positive constants and x is the displacement. Find the equilibrium position of the particle and discuss whether the equilibrium is stable, unstable or neutral?
In conservative field force F= – = – 
= – (2ax – b)
For equilibrium, F = 0
Or, – 2ax + b = 0
∴ x = 
Therefore, for x = the particle is inequilibrium position.
Again 
() = 
= 2a
Therefore, > 0 so, the particle is in stable equilibrium
Potential energy of spring: When a spring is compressed or elongated by a force F and the elongation or compression is x, then F 
x.
Or, F = kx [where k is the force constant of spring] ——-(i)
If Fe is the elastic force or restoring force applied by spring, then Fe = – kx [Fe is always towards the mean position].
Now the spring is further stretched through a distance dx, therefore the work done by the spring for further stretching is dw = -Fe.dx = Fedxcos 1800 = -Fedx = -kxdx [using equation (i)]
Therefore, the work done to stretched the spring through a distance x from its normal position(x = 0) is
W =∫dw =
kx dx = -k[
] = –
kx2 = potential energy of spring.
If spring is elongated from xi to xf, then work done by spring is w = – k(
– 
)
Conservation of energy of spring: When a spring is at unstretched condition, the potential energy of the spring is zero. Now F force is applied and the elongation of it is x and the potential energy of spring is kx2. At this time spring is at extreme position. Now the spring moves to its normal position due to elastic property, and at that condition total energy is kinetic energy i.e. kx2. When the spring is in extreme compressed position again total energy is converted to potential i.e. kx2 and this process continues. So, energy is conserved in vibrating spring.
.
Force constant of spring calculation:
- Spring in series: Two massless springs of force constant k1 and k2 are connected in series as shown in figure. Due to applied force F on the body the body is displaced by x. As the springs are massless, so the force acts on each spring is also F. If x1 and x2 are the elongation of two springs of force constant k1 and k2 respectively, then
F = k1x1 and F = k2x2.
But x1 + x2 = x. So, 
+ 
= x
If k is the equivalent force constant [replacing two springs by a single spring keeping force and elongation same] then + = 
Therefore, in series connection of spring 
= 
+ 
.
- Spring in parallel: (i) Two massless springs of force constant k1 and k2 are connected in parallel as shown in figure. Due to applied force F, the body is displaced by x.
Therefore, the elongation of each spring is also x.
If F1 and F2 are the force applied on two springs of force constant k1 and k2 respectively, then F1 = k1x and F2 = k2x.
Here F = F1 + F2 = k1x + k2x = (k1 + k2)x
If k is the equivalent force constant [replacing two spring by a single spring keeping force and elongation same] then, kx = (k1 + k2)x
Therefore, in parallel connection of spring k = k1 + k2.
(ii) In this figure when F force is applied on body towards right to displaced it by x, then spring k1 is expanded by x where F1 is the spring force produced. Similarly, spring k2 is compressed by x where F2 is the spring force.
Therefore, F = F1 + F2 = k1x + k2x = (k1 + k2)x
If k is the equivalent force constant [replacing two spring by a single spring keeping force and elongation same] then, kx = (k1 + k2)x
Therefore, the equivalent force constant k = k1 + k2.
Laws of conservation of mechanical energy:It state that the total mechanical energy of a system remain constant if only conservative forces are acting on the system of particles and the work done by all other forces is zero.
The initial potential and kinetic energy of the system are Ui and Ki respectively. The final potential and kinetic energy of the system are Uf and Kf respectively.
For conservative force the change in potential energy is equal to negative work done. So, – W = Uf – Ui
From work energy theorem, the work done on the system is the change in kinetic energy. So, W = Kf – Ki
Therefore, Ui – Uf = Kf – Ki
Ui + Ki = Uf + Kf
Therefore, in conservative field, total mechanical energy is conserved.
When non conservative forces like friction are acting on the system then total mechanical energy is not constant but work energy theorem is valid.
If conservative, non-conservative and external forces are acting on the system, then using work energy theorem we get, WC + WNC + Wext = Kf – Ki
But, – WC = Uf – Ui
So, WNC + Wext = Kf – Ki + Uf – Ui
Or, WNC + Wext = Kf + Uf – (Ki + Ui) = Ef – Ei = change in mechanical energy
Conservation of energy for freely falling body: Let us consider a body of mass m is placed at point A, at a height h from earth’s surface.
Potential energy at point A is P.E. = mgh
As the body is rest at A, then velocity at point A is 0. So, kinetic energy at point A is K.E. = 0
Total energy of body at point A is T.E. = P.E. + K.E. = mgh + 0 = mgh
Now the body is freely falling under gravity and at any instant it is at point B, at a height x from ground.
Potential energy at point B is P.E. = mgx [height = x]
Velocity of body at point B is vB then, vB2 = u2 + 2as = 2g(h-x) [as u = 0, a = g and displacement of body is (h –x)]
Kinetic energy of body at point B is K.E. = mvB2 = m2g(h-x) = mg(h-x)
Total energy of body at point B is T.E. = P.E. + K.E. = mgx + mg(h-x) = mgh
Now the body is at point C, just before touching the ground. So, height from ground is 0.
Potential energy at point C is P.E. = 0 [height = 0]
Velocity of body at point C is vC then, vC2 = u2 + 2as = 2gh [as u = 0, a = g and displacement of body from A is h]
Kinetic energy of body at point C is K.E. = mvC2 = m2gh = mgh
Total energy of body at point C is T.E. = P.E. + K.E. = 0 + mgx = mgh
Therefore, total energy remains same at all points on the freely falling motion of a body. So, mechanical energy is conserved.
Conservation of mechanical energy on smooth inclined plane: Let us consider a body of mass m is placed at point A on an inclined plane at height h from ground. The angle of inclination is .
The potential energy at point A is P.E. = mgh
As the body is initially at rest at that point, then the kinetic energy at point A is K.E. = 0.
The total energy at point A is T.E = mgh
Now the body is moving downward along the inclination with acceleration a = gsin. During its downward motion the body is at point D and the speed of the body at that point is v. DE is perpendicular on AC. The vertical downward displacement of the body at point D is AE = x.
The potential energy at point D is P.E. = mg(h – x)
Using the equation of motion v2 = u2 + 2as we get, v2 = 0 + 2gsinAD = 2gsin
= 2gAE = 2gx.
The kinetic energy at point D is K.E. = 
= 
= mgx
The total energy at point D is T.E = mg(h – x) + mgx = mgh.
Let us consider the speed of the body before touching the ground at point B is v/.
Therefore 
= 2gsinAB = 2gsin
= 2gAC = 2gh.
At point B the height of the body from ground is zero. So, potential energy at point B is P.E. = 0
The kinetic energy at point B is K.E. =
= 
= mgh
The total energy at point D is T.E = mgh
Therefore, the mechanical energy is conserved for a body moving on smooth inclined plane
- A body is displaced from point P to point Q. The kinetic energy and the potential energy of the body at point P and Q are given respectively KP =25 J, UP = -15 J, KQ = 5 J and UQ = 8 J.Find the work done by (i) conservative forces (ii) all forces (iii) forces other than conservative forces.
For conservative force the change in potential energy is equal to negative work done.
So, – WC = UQ – UP = 8 – (-15) = 23 J
WC = – 23 J.
According to work energy theorem, work done by all forces is equal to change in kinetic energy.
Wall = KQ – KP = 5 – 25 = – 20 J
Work done by forces other than conservative forces is equal to change in mechanical energy
Wother = KQ + UQ – (KP + UP) = (5 + 8) – (25-15) = 13 – 10 = 3 J.
- A weight less pan is fitted with a vertical spring as shown in figure. A block of mass m strikes the pan after falling through a height h. If the force constant of spring is k, then find the maximum compression of the spring.
Let us consider the maximum compression of the spring is x. Spring force and gravitational forces are conservative then using conservation of mechanical energy we get,
Ksi + Usi + KBi + UBi = Ksf + Usf + KBf + UBf
Or, 0 + 0 + 0 + mgh = 0 + + 0 + (-mgx)
Or, k
– 2mgx – 2mgh = 0
∴ x = = = ].
- A uniform chain of length L mass M is held on a frictionless table withnth(<1) part of its length hanging over the edge.When the chain is released, find the velocity of the chain while leaving the table.
Let us considered the surface of the table as the zero potential or reference level.
Initially the hanging part of the chain is nL. The centre of gravity of the hanging part of chain is at a distance 
from the reference level.
The initial potential energy of the hanging part of chain is Ui = -(
nL)g
= –
.
When the end part of the chain leaving the table at that instant the centre of gravity of the chain is at a distance of 
from the reference level.
Therefore, final potential energy of the hanging part of chain is Uf = –
.
Using conservation of energy we get, Ui + Ki = Uf + Kf
Or, – + 0 = – + 
∴ v =
.
- A block of mass 2m is suspended by a string of length l from celling. A bullet of mass m is moving horizontally and enters into the block. The block and the bullet move a maximum height. At the maximum height, the string creates angle 600 with vertical. If the string remains stretched at that condition find the tension on the string and the speed of the bullet before entering the block.
Let us consider the block is initially at point A and during maximum height it is at point B. BC is perpendicular on OA.
Therefore the maximum height h = AC = OA – OC = OA – OB cos600 = l(1 – cos600) = .
The speed of the block and bullet at point A [after bullet enters into the block] is v.
Using conservation of mechanical energy we get, kinetic energy at point A = potential energy at point B
Or, 
= (m+2m)gh
Or, 
= 
Or, v =
If the horizontal speed of the bullet before entering the block is u, then using conservation of linear momentum we get, mu + 2m = (m+2m)v
∴ u = 3v = 3.
If T is the tension of the string at point B, then Tcos600 = (m + 2m)g
∴ T = 6mg.
- A mass m is released from the top of a hemisphere (point P) of radius r with horizontal speed v. Calculate the angle with respect to the vertical where it leaves the contact from the hemisphere.
Let us consider, the mass will leave the contact from the hemisphere at point Q. If R is the reaction force acts on the mass by the hemisphere, then mgcos – R provides the required centripetal force to the mass during its circular motion. If at point Q, the speed of the mass is u, then mgcos – R = 
.
When the mass leave the contact from the hemisphere, then R = 0,
So, mgcos = .
cos = 
—– (i)
We draw a perpendicular on QS on PO. Therefore, SO = h = rcos.
Using conservation of energy at point P and Q we get, + mg(PS) = 
Or, + mg(r- rcos) =
Or, 
= 
+ 2gr(1- cos)
∴ u = 
Putting the value of u in equation (i) we get, cos = 
Or, cos = 
+ 2 – 2cos
Or, 3cos = + 2
∴ = 
[
+ 
]
Power: power is defined as the time rate of doing work. P = 
= 
= 
.
= Fvcos.
SI unit of power is watt = Nms-1 Dimension [P] =
=
= [ML2T-3].
1 horse power (H.P.) = The amount of power is required to hold a mass of 550 lb for 1 second at a height 1 ft from the surface of earth against the gravitational attraction of earth.
Example: 1. A car of mass m is moved upward on a rough inclined road of inclination . The coefficient of friction between wheel of the car and inclined road is μ. Find the power delivered by the car to move upward with constant speed v.
The net downward force acting on the car along the inclination is
F = component of weight of the car along the inclination + frictional force
Or, F = mgsin + mgcos = mg(sin + μcos)
As the car is moving upward with constant speed v, then the power delivered by the car is
P = Fv = mgv(sin + cos).
- An electric pump can lift a liter of water per second to a reservoir at a height h meter from ground. If the radius of the pipe through which the water is moved is b meter then calculate the velocity of water. Find the power delivered by the pump. [Neglect all resistive forces]
If the velocity of water is v then, volume of water is moved per second = area of pipedistance travelled by water per second
Or,
= a × 
∴ v = 
ms-1.
The pump can lift the volume of water per second is a liter = a×
cm3.
Mass of the water is lifted per second is m = a× gram = a kg [density of water = 1 gcm-3].
The potential energy per second of water due to move at a height h is EP = mgh = agh joule.
The kinetic energy of water per second is EK = 
= 
= 
joule.
Therefore the total energy of water per second is E = agh + joule.
Therefore power delivered by the pump is P = 
=
= agh + watt.
tag:
Share:
koushiadmin
