Displacement velocity (NEET JEE Main Advanced)

By Admin Koushi
(0) comments
June 25, 2025

Displacement velocity (NEET JEE Main Advanced)

CONCEPT: If initial velocity (u) is antiparallel to the acceleration (a) of the body, then the motion is retarded first and then accelerated.

Example: A ball is thrown vertically upwards with initial speed u. The time taken by the ball to travel maximum height is = .

If the given time t < , then distance(s) = displacement(s) = ut – g .

If the given time t = , then distance(s) = displacement(s) = ut – g .

If the given time t > , then displacement(s) = ut – g and

Distance (s) = + g . [Distance travelled by upward motion is = and distance travelled by downward motion in remaining time is = g .]

A particle starting from origin O(0,0,0) moves to point P (0,0,a) then moves point Q (0,a,a) then point R (0,a,0) then point S (a,a,0) and finally point T (a, a, a). Find the distance and displacement of the particle.

If the origin is O then distance s = OP + PQ + QR + RS + ST = a + a + a + a + a = 5a.

Displacement is OT = = = a.

Two balls A and B are projected vertically upwards with speed u and v from the top and the bottom of a tower of height h respectively. Find the meeting time of the balls [Neglect air resistance]

(a) Above the top of the tower:

Let us consider the balls meet after time t and taking upward motion is positive.

For ball A displacement = s₁, initial speed = u and acceleration = -g.

Then, S₁ = ut – gt² —– (i)

For ball B displacement = s₂, initial speed = v and acceleration = -g.

Then, S₂ = vt – gt² ——(ii)

From equation (i) and (ii) we get, S₁ + h = S₂

Or, ut – gt² + h = vt – gt² t = .

(b) In between top and bottom of the tower:

Let us consider the balls meet after time t and taking upward motion is positive.

For ball A displacement = – S₁, initial speed = u and acceleration = -g.

Then, – S₁ = ut – gt² or, S₁ = – ut + gt² —– (i)

For ball B displacement = s₂, initial speed = v and acceleration = -g.

Then, S₂ = vt – gt² ——(ii)

From equation (i) and (ii) we get, S₁ + S₂ = h

Or, – ut + gt² + vt – gt² = h

t = .

Let us consider the balls meet after time t and taking upward motion is positive.

For ball A displacement = – S₁, initial speed = u and acceleration = -g.

Then, – S₁ = ut – gt² or, S₁ = – ut + gt² —– (i)

For ball B displacement = – s₂, initial speed = v and acceleration = -g.

Then, – S₂ = vt – gt² or, S₂ = – vt + gt² ——(ii)

From equation (i) and (ii) we get, S₁ – S₂= h

Or, – ut + gt² + vt – gt² = h

t = .

CONDITIONS OF MINIMUM DISTANCE BETWEEN TWO BODIES: Two cars A and B are moving along a straight line in same direction separated by a distance. Car B is behind car A. The instantaneous speed of cars A and B are respectively v₁ and v₂.

If v₁ > v₂, then the distance between the cars increases.

If v₁ < v₂ , then the distance between the cars decreases.

If v₁ = v₂, then the distance between the cars is minimum.

EXAMPLE: Two cars A and B (B is behind A) separated by a distance 200m moving along the same direction with initial speed 3ms^-1 and 9ms^-1 respectively. The acceleration of car A and car B are respectively 4ms^-2 and 2ms^-2 . When the separation between the cars is minimum and what is the minimum distance?

The distance between the cars is minimum when v_A = v_B and the time is t.

v_{A =} 3 + 4t and v_B = 9 + 2t so, 3 + 4t = 9 + 2t or, t = 3s.

Distance travelled by car A for 3s is s_A = 3 3 + 4 3² = 27 m

Distance travelled by car B for 3s is s_B = 9 3 + 2 3² = 36 m

Minimum distance = 200 + s_A – s_B = 200 + 27 – 36 = 191 m.

TWO DIMENSIONAL MOTION:

A body of mass m is moving with constant speed u along x axis and F force is applied on it along y axis. Find velocity of it after t second and trajectory.

Along x axis: initial speed u_x = u acceleration a = 0 velocity after t second

v_x = u_x = u ——–(i)

and distance travelled x = ut ——-(ii)

Along y axis: initial speed u_y = u cos 90⁰ = 0 acceleration a = velocity after t second

v_y = u_y + at = ——(iii)

and distance travelled y = u_yt + at² = ——-(iv)

Velocity of the body is v = = 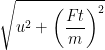if the velocity of the body creates angle with positive x axis then, tan = = .

Trajectory: From equation (ii) t = and using the value of t in equation (iv) we get, y = .

The initial velocity of a body is = a + b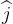 and acceleration is 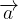= c +d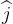 Find the displacement of the body.

Displacement of the body is =t + = (a+ b)t +(c+d ) = (at+ c) +( bt +d)

CONCEPT ON MOVING FRAME: When a reference frame is moving and a body is dropped from that frame, then that body also gains the instantaneous speed of that frame.

A lift moving upwards with speed u. When the lift is at a height h from ground a ball is dropped from it. Find the time taken by the ball to touch the ground.

Let the time is t and taking downward direction is positive. h = – ut + g t²

Or, gt² – 2ut –2h = 0

Or, t =

t = [as time cannot be negative].

A lift moving upwards with speed u. When the lift is at a height h from ground a boy throws a ball vertically upwards with speed v from it. Find the time taken by the ball to touch the ground.

Let the time is t and taking downward direction is positive. The speed of the ball from the lift is w = (u + v) then,

h = – wt + gt²

Or, gt² – 2wt –2h = 0

Or, t =

t = [as time cannot be negative].

A lift moving upwards with speed u. When the lift is at a height h from ground a boy throws a ball vertically downwards with speed v (v > u) from it. Find the time taken by the ball to touch the ground.

Let the time is t and taking downward direction is positive. The speed of the ball from the lift is w = (v-u) then,

h = wt + gt² or, gt² + 2wt –2h = 0 or, t = t = [as time cannot be negative].

CONCEPT ON VELOCITY:

The length of the minute hand of a clock is r cm. Calculate the magnitude of change in velocity of the tip of the minute hand from 12 noon to 12.15 pm.

The speed of the minute hand of a clock is v = = = cm

When the minute hand of a clock is at 12noon the direction of velocity () is towards +ve x axis. When the minute hand of a clock is at 12.15pm the direction of velocity ( ) is towards -ve y axis. Using vector subtraction method the change in velocity is ( – )

= = cm. [Magnitude of or is || = ||= ].

A particle is moving with constant speed v in a circular path of radius r. It creates angle at the centre when moves from point A to B along the circumference of the circle. Find the change in velocity of the particle: At point A velocity of the particle is v_A (magnitude = v) and direction is along the tangent AC. Similarly at point B velocity of the particle is v_B (magnitude = v) and direction is along the tangent BD.

Draw a perpendicular AE on OB. Then EAF = as AE and FB are parallel and AC is the intersection then, CFB = . Therefore, the angle between v_A and v_B is .

So, change in velocity

of the particle is

Δv = [using vector subtraction rule( – )]

= v

= vsin

= 2v sin.

Average acceleration of the particle: The time taken to travel the distance AB is t, then = t = or, t =

Average acceleration = = = sin .

In the figure, the blocks A and B are of equal mass connected by a massless inextensible string over a pulley P which is frictionless. At any instant Block A moves on a horizontal surface with speed V_A and string creates angle with it. At that time B is moving with speed V_B. Find the relation between V_A and V_B.

Let the lengths of the sections of the string be AP = l₁ and PB = l₂ then the total length of the string is (l₁ + l₂).

In a further time t, let A moves to the right (point A^/) by x and B move down (point B^/) by y.

A^/C is perpendicular on AP.

Now A^/P PC = PA – AC = PA – AA^/ = l₁ – x and PB^/ = l₂ + y.

So, the total length of the string is A^/P + PB^/ = l₁ – x + l₂ + y = (l₁ + l₂ – x + y).

Therefore, l₁ + l₂ = l₁ + l₂ – x + y

Or, x = y

Differentiating both side of equation with respect to time t we get,

Or, =

V_A= V_B [The velocities of A and B are respectively V_A = and V_B = .]

A particle slides without friction from the highest point A of a vertical circle along a chord. If the particle starts from rest, show that the time of descent is independent of the chord chosen.

Let the radius of the circle is R. If the particle slides along the chord AB as shown in the figure, then the component of acceleration due to gravity along AB is gcos .

The length AB = 2AC = 2AOcos . = 2Rcos . [where is the angle made by AB with the vertical diameter.]

Using the equation s = a we get, 2Rcos . = gcos . or, t = .

So, the time of descent of the particle is independent of the chord chosen.

Motion (Jee advanced)

Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time

t = 0. Each of the particles moves with constant speed u. A always has its velocity along AB, B along BC and C along CA. Find the time when the particles meet each other.

Velocity of A is always along AB. Velocity of B is always along BC. So component of B along BA is vcos60° = . Thus, the separation AB decreases. The relative speed of A with respect to B along AB is v + = .

Time taken to reduce the distance AB (= d) is t = = .

Four boys A, B, C and D are initially at rest at four corners of a square of each side a. Each boys are moving with a uniform speed v in such a way that A always moves towards B, B always moves towards C, C always moves towards D and D always moves towards A. Where and at what time will they meet?

At any moment four boys are at the corner of a square whose sides are gradually decreases and finally meet at centre O. The velocity of A is v along AB and velocity of B is v along BC. So the velocity of B along A is vcos = 0 (as AB and BC are perpendicular)Thus, the separation AB decreases at a rate

of v + 0 = v. So, the time taken in reducing the separation AB from a to zero is t = .

In the figure, the pulley P moves to the right horizontally with a constant speed u. The downward speed of block B is V_B, and block A is moving on horizontal plane to the right with speed V_A. Find the relation between V_A and V_B.

At any instance of time, let the length of the string AP = l₁ and the length PB = l₂. In a further time t, let A moves to the right (point A^/) by x and B move down (point B^/) by y, while P moves to the right (point P^/) by ut. The velocities of A and B are respectively V_A = and V_B = .

As the length of the string must remain constant, AP + PB = A^/P^/ + P^/B^/

Or, l₁ + l₂ = (l₁ – x + ut) + (l₂ + y)

Or, x = ut + y

Differentiating both side of equation with respect to time t we get,

Or = +

V_A= u + V_B.

In the figure, the blocks A and B are of equal mass connected by a massless inextensible string over a pulley P which is frictionless. At any instance Block A moves on a horizontal surface with speed V_A and string creates angle with it. At that time B is moving with speed V_B. Find the relation between V_A and V_B.

Let the lengths of the sections of the string be AP = l₁ and PB = l₂ then the total length of the string is (l₁ + l₂).

In a further time t, let A moves to the right (point A^/) by x and B move down (point B^/) by y.

A^/C is perpendicular on AP.

Now A^/P ≈ PC = PA – AC = PA – AA^{/ cos} = l₁ – x cos and PB^/ = l₂ + y.

So, the total length of the string is A^/P + PB^/ = l₁ – x cos + l₂ + y = (l₁ + l₂ – x cos + y).

Therefore, l₁ + l₂ = l₁ + l₂ – x cos + y

Or, x cos = y

Differentiating both side of equation with respect to time t we get,

Or, =

V_{A cos}= V_B [The velocities of A and B are respectively V_A = and V_B = .]

The time taken by a particle to slide down an inclined plane is least along the line of greatest slope.

Let us consider an inclined plane of height h and angle of inclination is . A particle is released from the top (point A) of the inclined plane slide down along the greatest slope AB. The acceleration of the particle along AB is a = g sin and the travel time is t₁. Then using the relation for line AB is s = ut + at² we get, = g sin

Or, t₁ = = cosec .

Another particle is slides down from point A to C. The distance AC = AB sec = h cosec sec . Acceleration along AC is a = (g sin)cos and the travel time is t₂. Then using the relation for line AC is s = ut + at² we get,

hcosec sec = g sincos

Or, t₂ =

∴ t₂ =cosec sec = t₁ sec .

As sec >1 [as 0<<]

so, t_{2 > t1}

RAIN – MAN CONCEPT:

(i) Man is moving on horizontal surface with constant speed:A man is moving on horizontal surface with constant speed V_M = u and rain is falling vertically with speed V_R = v. Find the velocity of rain with respect to man and at what angle with the vertical the man holds umbrella to protect him?

We know that = –

So, = = .

Rain is falling at an angle θ = () =() . Therefore the velocity of rain with respect to man is and the man holds umbrella at an angle θ = () with the vertical.

CONCEPTS ON SHORTEST DISTANCE: 1. Two ships A and B are at a distance d apart along the line in north-south direction. Ship A is situated to the north of ship B and is moving due west with a speed v. Ship Bis moving towards north with speed v. Find out the distance of closest approach between them and also calculate the time required to come to this position.

[As two velocity vectors have different origin, then we have to represent those vectors from a common origin.]

Velocity of ship B with respect to ship A is = – or, = = 2v (along BC) and creates angle φ with . So, tanφ = = = or,φ = 30⁰

Let AC is perpendicular on BC and AC is the shortest distance between two ships. So, AC = AB sinφ = d sin = .

The time required to come to this position is t = = = = = . [As we know the velocity along BC, we consider the time to move from B to C.]

Two cars A and B are moving with speed u and v respectively along two mutually perpendicular straight lines as shown in figure. What is the minimum distance between two cars?

Let us consider two cars are at a distance a and b respectively from point O and after time t the distance between two cars is minimum when they are at position A^/ and B^/ respectively. If L is the minimum distance between two cars then, = +