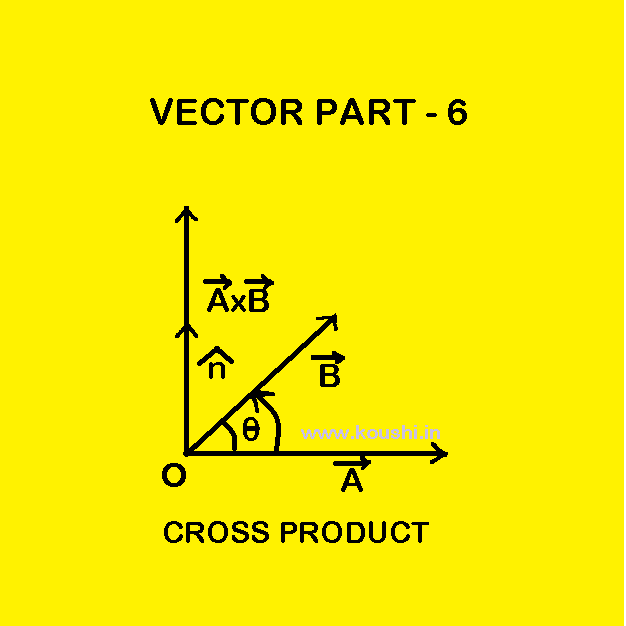
Vector product or cross product: The vector product of two vectors 
and 
is defined as the product of the magnitudes of and and the sine of the angle between them.
If and creates angle θ then 
= AB
. Where 
is the unit vector perpendicular to the plane of and .
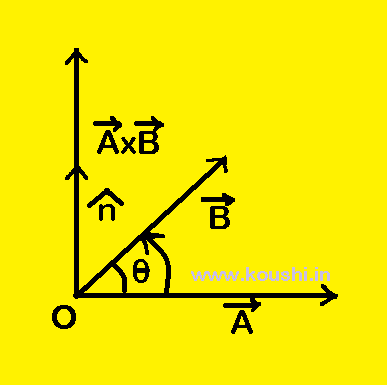
Properties of cross product:
= BA (-) and ||= BA
= AB = ||
(ii) If the angle between and is 
then = ABsin = 0
(iii) = A.Asin = 0
(iv) If the angle between and is 
then = ABsin = AB.
(v) 
= 
= 
= 1.1sin = 0
(vi) = , = , = .
Concepts on dot product
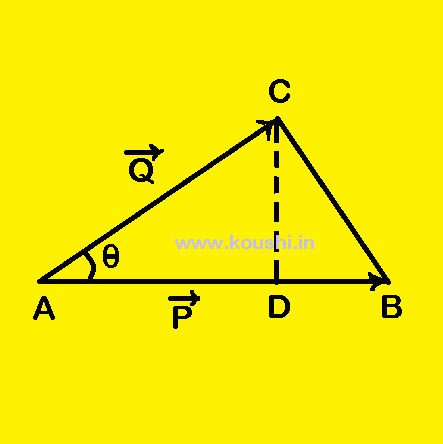
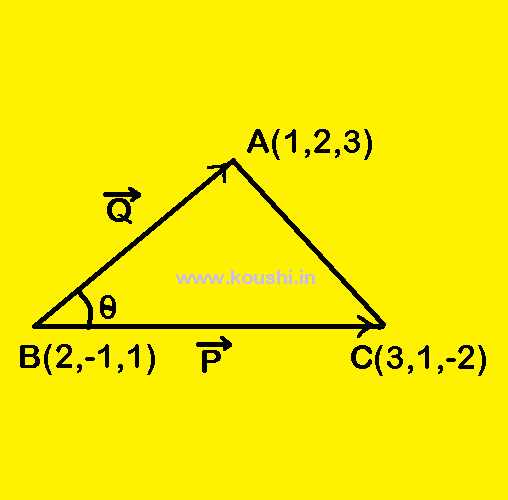
1. Area:
Area of a triangle: 
and 
are represented by two sides AB and AC of 
ABC and CD is perpendicular to AB. Angle between and is 
.
The area of ABC = 
CD.AB = ACsin AB = QsinP = PQsin = | 
|.
The direction of area vector is perpendicular outward to the plane of the triangle.
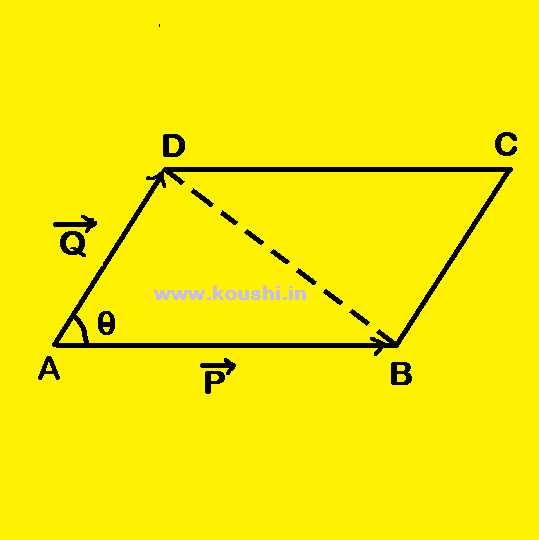
Area of a parallelogram: ABCD is a parallelogram whose sides AB and AD are represented by and .
Area of a parallelogram = 2 Area of a triangle = 2 | | = | |.
Example: ABC is a triangle and the coordinates of vertices A, B and C are respectively (1, 2, 3), (2, -1, 1) and (3, 1, -2). Find the area of ABC.
= 
= (3 -2)î + (1+1)ĵ + (-2-1)k̂ = î + 2ĵ -3k̂and = 
= (1-2)î + (2+1)ĵ + (3-1)k̂ = – î + 3ĵ +2k̂.
The area of ABC = | |
= 
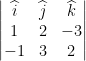= (4+9)î + (+3-2)ĵ + (3+2)k̂ = 13î + ĵ + 5k̂.
| | = 
= 
.
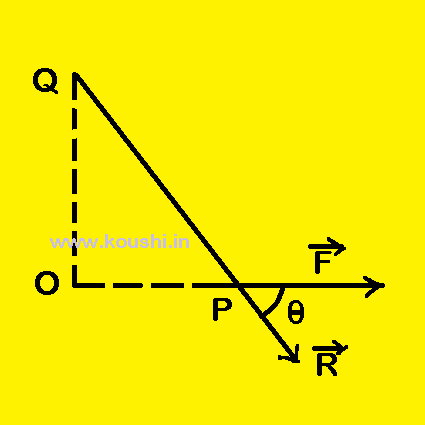
2. Torque: Torque or moment of force about point Q = Force at point P Perpendicular distance QO = F QPsin = FRsin = RFsin
= 
. The direction of torque is perpendicular outward to the plane of and .
Example: Force = 2î + 3ĵ – k̂ acts at point P (1, 2, 3). Find torque about point Q (2, 1, 1).
= 
= (1 -2)î + (2-1)ĵ + (3-1)k̂ = -î + ĵ + 2k̂
= = 
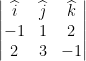= (-1-6)î + (4-1)ĵ + (-3-2)k̂ = -7î + 3ĵ – 5k̂.
3. Perpendicular unit vector: What is the perpendicular unit vector of 
= î +2ĵ – k̂ and 
= 2î + ĵ + 2k̂?
The perpendicular vector of and is 
= | |= 
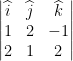= (4+1)î + (-2-2)ĵ + (1-4)k̂ = 5î -4ĵ -3k̂.
Unit vector of is 
= 
= 
= 
.
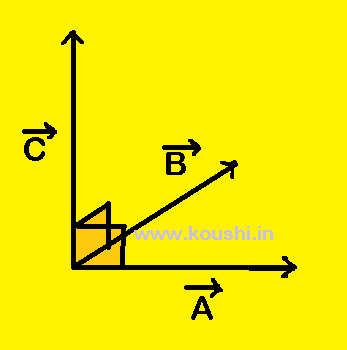
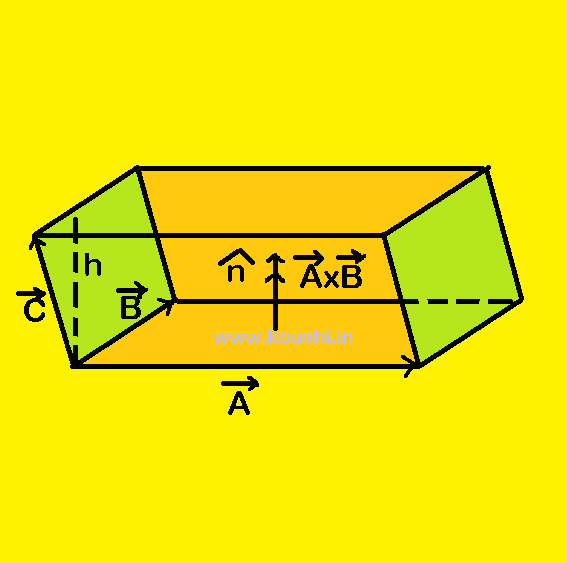
4. Volume of a parallelopiped: The three sides of a parallelepiped are represented by , and . Area of base of parallelepiped (parallelogram) is = | |
where is the unit vector perpendicular to base of parallelepiped.
Height h of the parallelepiped is h = . (projection of on .)
Volume of parallelepiped = height area = .| | = .( )
Vector triple product: .( ) = .( ) = .( )
If = 
, = 
and = 
then,
.( ) = 
= – 
= 
= .( )
.( ) = = – 
= 
= .( 
)
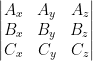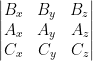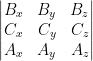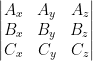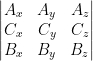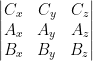Therefore, .( ) = .( ) = .( ).
.( ) = = 
+ 
+ 
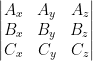If , and are coplanar then .( ) = 0.
Example: What is the value of a, for which = (4î –ĵ +3k̂), = (2î +ĵ -2k̂) and = (aî + ĵ – k̂) are the coplanar vectors?
Here .( ) = 0
Or, 
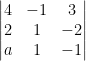= 0
Or, 4(-1+2) -1(-2a +2) +3(2-a) = 0
Or, 4+2a-2+6-3a = 0
a = 8.
5. Equation of a plane and distance of plane from origin:
= 2î+3ĵ+2k̂ is perpendicular to a plane. The terminal point of another vector = î+2ĵ+k̂ touches the plane. Find the equation of the plane.
Let us consider Q is a point on the plane with coordinates (x, y, z). The position vector of point Q is xî + yĵ + zk̂.
= (1 – x)î + (2 – y)ĵ+(1 – z)k̂ is lying on the plane which is perpendicular to .
Therefore, . = 0
Or, (2î + 3ĵ + 2k̂).[(1 – x)î + (2 – y)ĵ + (1 – z)k̂] = 0
Or, 2(1 – x) + 3(2 – y) + 2(1 – z) = 0
Or, 2 – 2x + 6 – 3y + 2 – 2z = 0
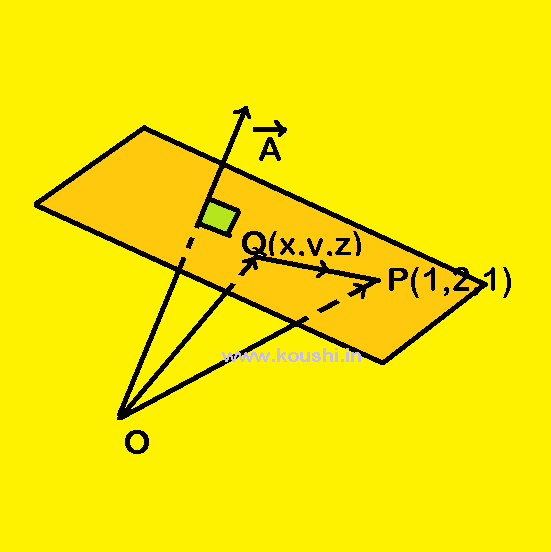
2x + 3y + 2z = 10
The distance of plane from origin is projection of on 
= .
= 
= 
.