

Work Energy Power Part 1
tag:
Share:
Admin Koushi


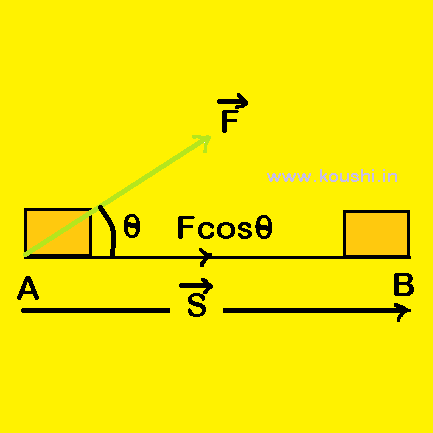
Work: Work is said to be done when a force is applied on a body and the body is displaced through a certain distance in the direction of the applied force.
If F is the force is applied on a body at an angle θ with displacement S, then work done on the body is W = Fcos![]() S =
S = ![]() .
.
Unit: SI unit of work is joule (J) = 1newton![]() 1meter
1meter
C.G.S. unit of work is erg = 1dyne![]() 1centimeter
1centimeter
1J = 105dyne![]() 102cm = 107erg.
102cm = 107erg.
Dimension of work [W] = [F][S] = [MLT-2][L] = [ML2 T-2].
Positive work: If force (or its component) and displacement are in same direction (00 < θ <900) then the work done is positive. Example: A body is falling vertically under gravity.
Negative work: If force (or its component) and displacement are in opposite direction (900 < θ <1800) then the work done is negative. Example: A body is projected vertically upward against gravity.
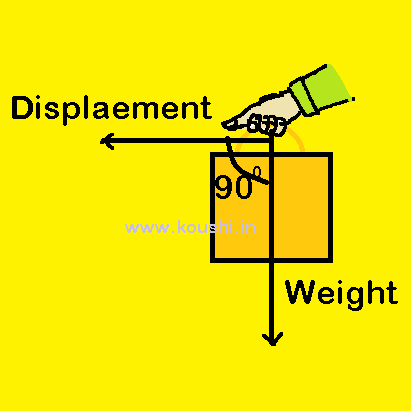
Zero work: If force and displacement are in perpendicular direction (θ = 900) then the work done is zero and the force is called no work force. Example: A man holds a suitcase in his hand moves in horizontal road.
If the displacement of the body or applied force on it is zero then also the work done is zero.
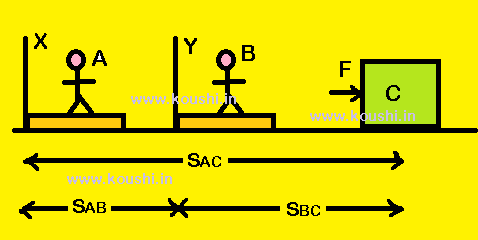
Work done on a body is different depending on the frame of reference:
Let us consider observer A and B are fixed with two reference frame (inertial) X and Y respectively. A force F is applied on a block C. Let us consider ![]() and
and ![]() are the work done with respect to observe A and B respectively whenever F force is acting on the block.
are the work done with respect to observe A and B respectively whenever F force is acting on the block.
If ![]() and
and ![]() are the displacement observed by observer A and B respectively for any interval of time, then the corresponding work done is given by
are the displacement observed by observer A and B respectively for any interval of time, then the corresponding work done is given by ![]() =
= ![]() .
.![]() and
and ![]() =
= ![]() .
.![]() .
.
Therefore, if same force is applied on a body then work done are different relative to different frame of reference.
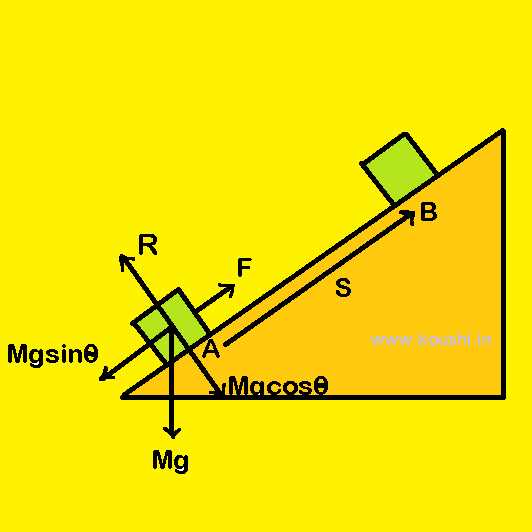
Example: A block of mass M is placed on an incline plane of inclination ![]() . It is moved upward direction from A to B by a constant force F acting parallel to the incline plane. Calculate the work done by the gravitational force, external force F and also calculate the net work done.
. It is moved upward direction from A to B by a constant force F acting parallel to the incline plane. Calculate the work done by the gravitational force, external force F and also calculate the net work done.
R is the normal reaction applied by the inclined surface on the block. If we resolute the weight of the block mg, R = Mgcos![]() .
.
Here R and Mgcos![]() are perpendicular to the displacement of the block AB (= s). So, they does not perform any work.
are perpendicular to the displacement of the block AB (= s). So, they does not perform any work.
The work done due to gravitational force to move the block from A to B is Wgravitational = Mgsin![]() scos1800 = – Mgssin
scos1800 = – Mgssin![]() .
.
The work done by the external force F to move the block from A to B is Wexternal = Fscos00 = Fs.
The network done on the block is Wnet = (F – Mgsin![]() )s.
)s.
Work done by the pair of interactive force: The interacting forces like electrostatic force, gravitational force of attraction, spring force, friction etc. can perform work on a system.
Let us consider two particles A and B interact with each other by a pair of action reaction forces ![]() and –
and –![]() respectively.
respectively.
Also consider dxA and dxB are the elementary displacement of the particles A and B respectively.
Work done on particle A is dwA = FdxA
Work done on particle B is dwB = -FdxB
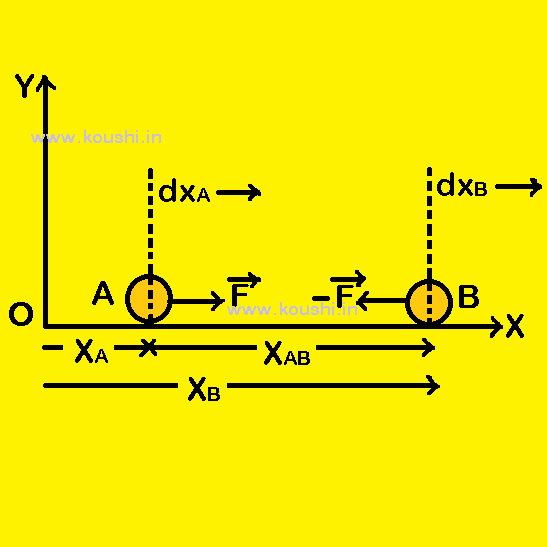
Total work done on the system for elementary displacement is dw = dwA + dwB = F(dxA – dxB) = FdxAB —– (i0
Where dxAB is the elementary displacement of particle A with respect to particle B.
The relative displacement is zero under constrain forces like tension on inextensible string.
Work done is represented by the area under force versus displacement graph.
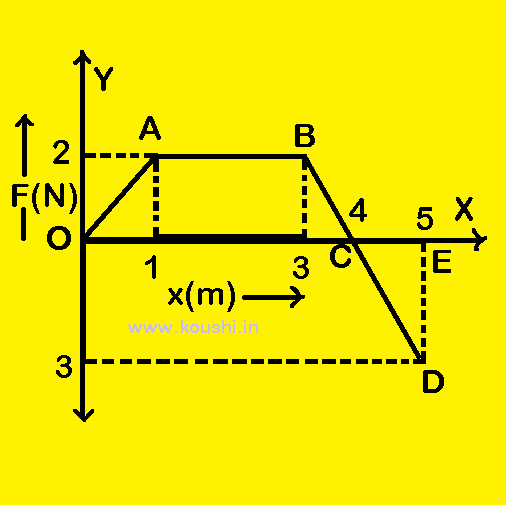
Example: The variation of applied force F with displacement x of a particle is given in the graph. Calculate the work done of the particle for the displacement of 5m.
The total work done of the particle consists of two parts. One is positive work done W1 and the other is negative work done W2.
W1 = area of the trapezium OABC = ![]() [2+4]2 = 6 J.
[2+4]2 = 6 J.
W2 = area of triangle CDE = ![]()
![]() (-3)
(-3)![]() 1 = – 1.5 J.
1 = – 1.5 J.
The total work done of the particle is W = W1 + W2 = 6 -1.5 = 4.5 J.
© 2018 – 2025 Koushi All Rights Reserved