Work energy theorem: Work done by all forces like conservative, non-conservative, external, internal acting on a particle is equal to the change in kinetic energy of it.
Therefore, according to work energy theorem we can say that the work done by the resultant force acting on the particle (which is equal to the sum of work done by individual forces) is equal to the change in kinetic energy of it.
If the total work done is positive then the kinetic energy will increase and if work done is negative then the kinetic energy will decrease.
Let us consider a body of mass m is moving with initially speed u. It is applied by an external force F and the velocity of the body is v after travelling a distance s. The acceleration of the body is a = 
.
Then v2 = u2 + 2as
Or, v2 – u2 = 
Or, Fs = 
Or, W = change in K.E. of the body.
Work energy theorem for variable forces: The work done by a force on a body is equal to the change in kinetic energy of the body.
Let us consider a body of mass m is moving with initially speed v and the kinetic energy of the body is E = 
mv2
Differentiating both side with respect to time t, we get 
 = 
[mv2] = m2v
 = mv = mva [acceleration a = ]
Or, Â = ma
 [as v = ]
Or, dE = Fdx = dw ——-(1)
When x = xi, KE = (KE)I and w = 0 and when x = xf,, KE = (KE)f and w = W
Integrating both side of equation (1), we get, 
dE = 
dw Â
Or, [(KE)f – (KE)i] = W
So, the work done by a force on a body is equal to the change in kinetic energy of the body.
Work energy theorem is also applicable for non-inertial frame of reference. At that case we have to consider the work done by the pseudo force also.
Example: 1. A plank of mass M is on a frictionless horizontal surface is applied by a constant force F. Another block of mass m is placed on the plank. There is no relative displacement between plank and block. We can consider the following conditions.
.
The frictional force generates in between the surface of block and plank. The frictional force acting on block by plank is in forward direction and it is f = ma = 
. 
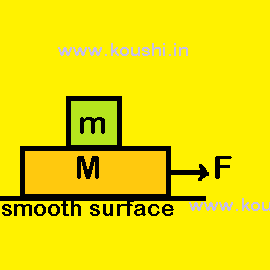
Observed from ground (inertial frame of reference): As there is no relative displacement between block and plank, therefore block and plank move distance s and at that instant velocity is v.
The work done by the friction on the block is Wf = fs = 
.
From work energy theorem, Wf = K.E.f – K.E.i
Or, fs = 
Or, Â =
 v =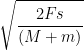 
.
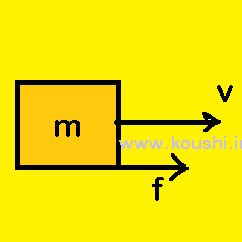
Observed from plank (non-inertial frame of reference): In this case pseudo force acting on the block which is equal to frictional force as there is no displacement of block with respect to plank.
Therefore, total work done W = Wf + WP = Â – Â = 0 [pseudo force is opposite to the displacement hence the work done due to pseudo force is negative]
From work energy theorem, W = change in K.E.
Or, 
 = 0
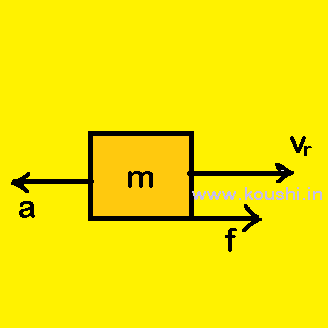
 vr = 0 [vr is the velocity of block relative to plank].
2. A body of mass m is slowly moved up through a curved surface from position A to B by a force F which is directed at each point along the tangent to the trajectory. Find the work done performed by this force if the height of point B is h and horizontal length of the base is L. The coefficient of friction is 
.
There are four forces acting on the body, (i) weight of the body (ii) normal reaction applied by the surface on body, (iii) frictional force (iv) applied force.
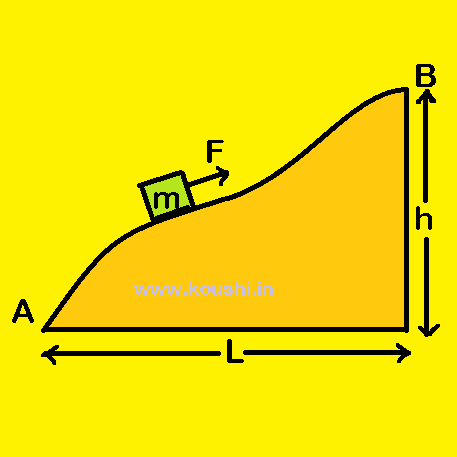
Using work energy theorem we get, the work done by all forces = change in kinetic energy
Therefore, Wmg + WN + Wfriction + WF = 
K.E. ——— (i)
As gravitational force is conservative force, then – Wmg = Uf – Ui = mgh – 0
Or, Wmg = – mgh.
Normal reaction at all points is perpendicular to the displacement, then the work done by normal reaction is zero. So, WN = 0
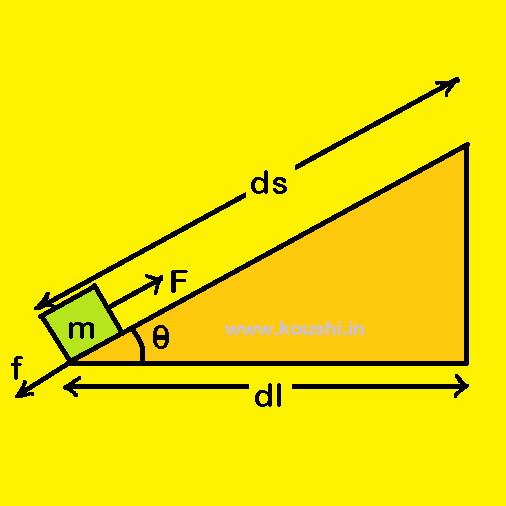
Frictional force f = mgcos
The work done by the frictional force for the displacement ds isÂ
dw = 
mgcosds = – mgdl.
The work done by the frictional force to displace the body from point A to point B is W = 
dWÂ = 
–mgdl = – mgL.
From equation (i) we get, – mgh – mgLÂ + WF = 0
WF = mg(h + L).
