Conservative and non-conservative field: A force is said to be conservative if the work done by or against the force in moving a body depends only on the initial and final position of the body not the nature of the path. Gravitational force, electrostatic force between two stationary charges, spring force etc. are conservative force.
Gravitational force is a conservative force because if we move a particle of mass m against gravity for a height h then the potential energy is –mgh. It does not depend on path. It depends only the initial and final position of the particle.
Magnetic field is neither conservative nor non-conservative.
When electric field is produced by static charge, it is conservative. When electric field is produced by time varying magnetic field then it is non-conservative.
For conservative force, work done is path independent. Work done in a closed path is zero. For conservative force, work done is equal to change in potential energy.
A force is said to be non-conservative if the work done by or against the force in moving a body depends upon the initial and final position of the body and the nature of the path. Frictional force, viscous force etc. are non-conservative force.
For non-conservative force, work done depends on path. For a closed path work done is not zero. For non-conservative force work done is not equal to change in potential energy.
Potential energy: The energy possesses by a body by virtue of its position or configuration (shape) is called potential energy. Potential energy is defined as the work done by a conservative force. Force always do positive work at the expense of its potential energy stored in the field. The loss of potential energy is equal to the total work done by the conservative forces.
Whenever the elongation or compression of a spring decreases, the spring force decreases it means that the work done by the spring is equal to the loss of its potential energy.
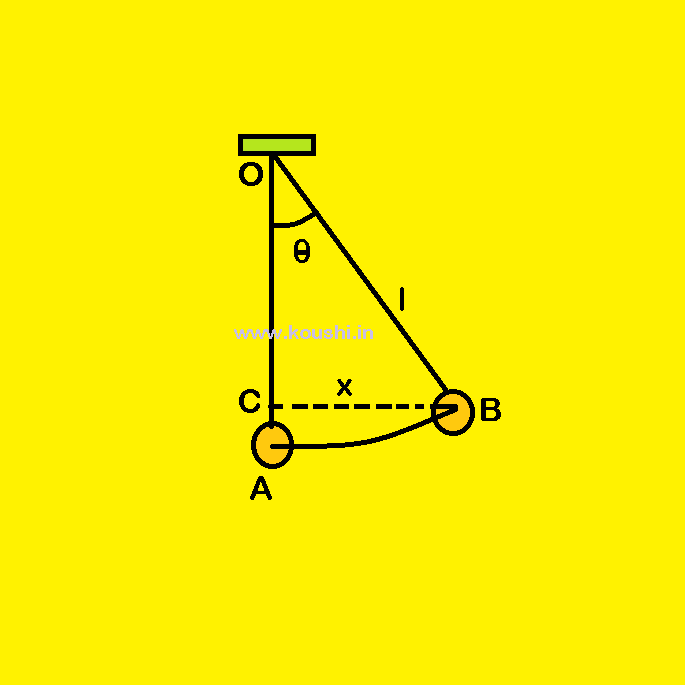
Example: A pendulum initially is at rest position at point A. If the bob is pulled slowly towards right at point B, find the change in gravitational potential energy of the pendulum as a function of x. The effective length of the pendulum is l and mass of the bob is m.
When the bob is at point B then the vertical height travel by the bob from initial point A is h.
If the string of the pendulum creates an angle 
with the vertical at point B, then cos = 
= 
.
Initial potential energy of the bob at point A = 0
Final potential energy of the bob at point B = mgAC = mg(OA – OC)
= mgl(1- cos)
= mgl(1- ).
Change in potential energy of the bob is mgl(1- ).
Relation between conservative force with potential energy: Change in potential energy of a particle between two points in the conservative field is defined as the work done by the associated conservative force to displace the particle between those two points without any change in kinetic energy.
Let us consider two points A and B in a conservative field are separated by infinitesimal distance dr. A particle is moved in between two points by conservative force F. The potential energy at those points are respectively UA and UB. The work done required to move the particle from point A to point B is dW = Fdr. The change in potential energy is dU = UB – UA
Therefore, dU = – Fdr
Or, F = – 
Or, 
U = Uf – Ui = – 
.
= – W
If we consider the reference point at infinity, then the potential energy at infinity is zero.
So, U = Uf – 
= – 
. = – W.
In Cartesian co-ordinate system the components of a force is in x, y, z axes can be given as the negative gradient of potential energy measured along the corresponding axes.
Therefore, 
= – 
, 
= – 
and 
= – 
So, = – ( + + )
Where is the partial differentiation of U with respect to x when y and z are constant.
is the partial differentiation of U with respect to y when x and z are constant.
is the partial differentiation of U with respect to z when x and y are constant.
Potential energy graph: The variation of potential energy with displacement is shown in graph. The force acting on the particle is defined as the negative gradient of potential energy (F = – ).
We can consider the following factors from the graph.
In the region from AB, the potential energy decreases with increase of x. Therefore, 
is negative and the direction of F is positive i.e. repulsive in nature.
In the region BC, the potential energy increases with increase of x. Therefore, is positive and the direction of F is negative i.e. attractive in nature.
At point B, C and D is zero therefore no force is acting at these points, hence the particle is in equilibrium at those points.
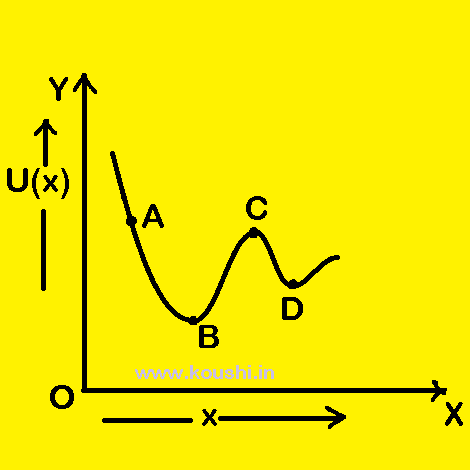
The potential energy of the particle changes with displacement is given in the graph. The stability of the particle is explained from the graph. Let us consider some points on the graph.
Stable equilibrium: Let us consider points 1 and 2 very close to point A. At point 1 potential energy decreases with increase of x. Therefore, < 0 and force F1 (= – ) is positive in direction. Similarly at point 2 potential energy increases with increase of x. Therefore, > 0 and force F2 (= – ) is negative in direction. The slope changes from negative to positive at point A when we move along positive x direction. The direction of force changes from positive to negative at point A. Therefore it indicates that the force is always towards that point A. If the particle which is at point A is slightly displaced, it always return to point A.
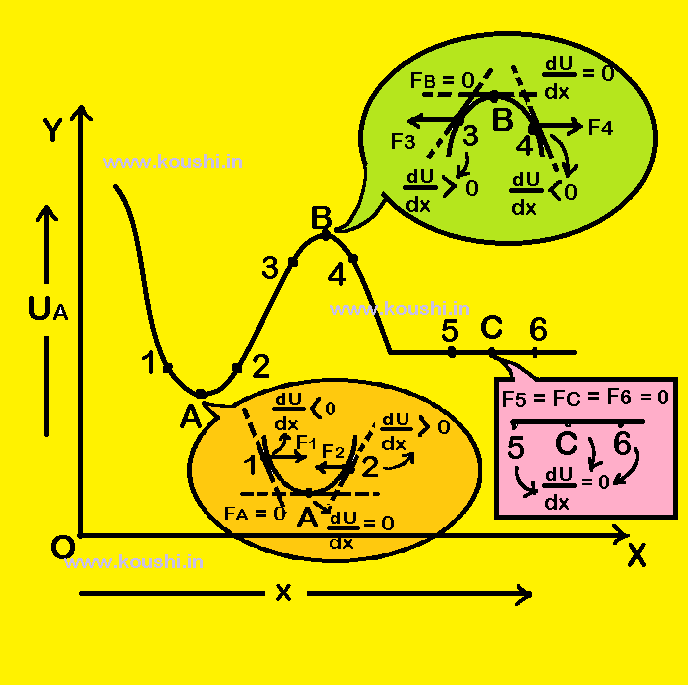
Therefore, at point A the particle is in stable equilibrium. The condition of stable equilibrium is = 0 and 
> 0.
Unstable equilibrium: Let us consider points 3 and 4 very close to point B. At point 3 potential energy increase with increase of x. Therefore, > 0 and force F3 (= – ) is negative in direction. Similarly at point 4 potential energy decreases with increase of x. Therefore, < 0 and force F4 (= – ) is positive in direction. The slope changes from positive to negative at point B when we move along positive x direction. The direction of force changes from negative to positive at point B. Therefore it indicates that the force is always away from point B. If the particle which is at point B is slightly displaced, it will never come to that point. Therefore, at point B the particle is in unstable equilibrium.
The condition of unstable equilibrium is = 0 and < 0.
Neutral equilibrium: Let us consider two points 5 and 6 very close to point C. At point C there is no change of potential energy with respect to x. Therefore, = 0 and the particle experience zero force when it is displaced near point C. At that condition we can say that particle is in neutral equilibrium.
Example: The potential energy of a particle in conservative force field is given by U = ax2 – bx, where a and b are the positive constants and x is the displacement. Find the equilibrium position of the particle and discuss whether the equilibrium is stable, unstable or neutral?
In conservative field force F = – = – 
= – (2ax – b)
For equilibrium, F = 0
Or, – 2ax + b = 0
x = 
Therefore, for x = the particle is in equilibrium position.
Again = 
= 2a
Therefore, > 0 so, the particle is in stable equilibrium.