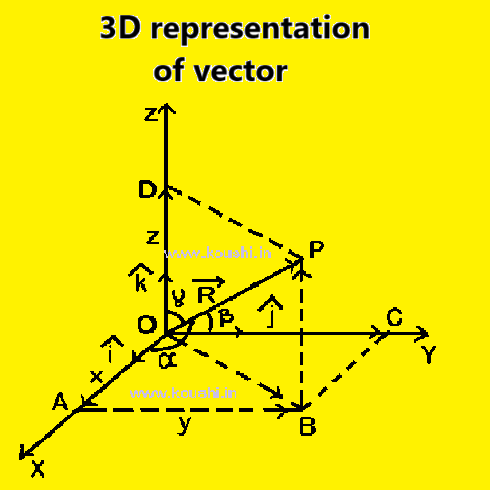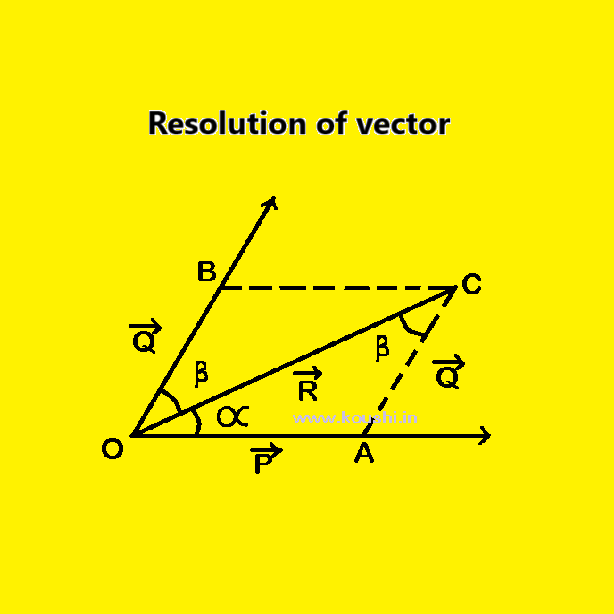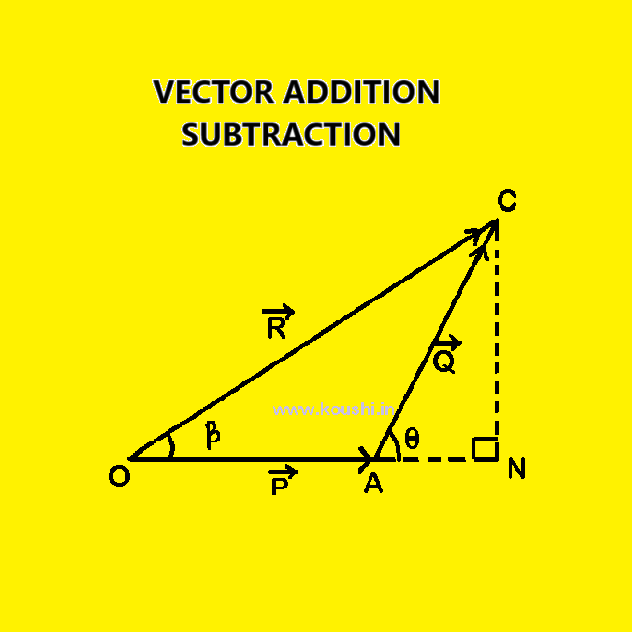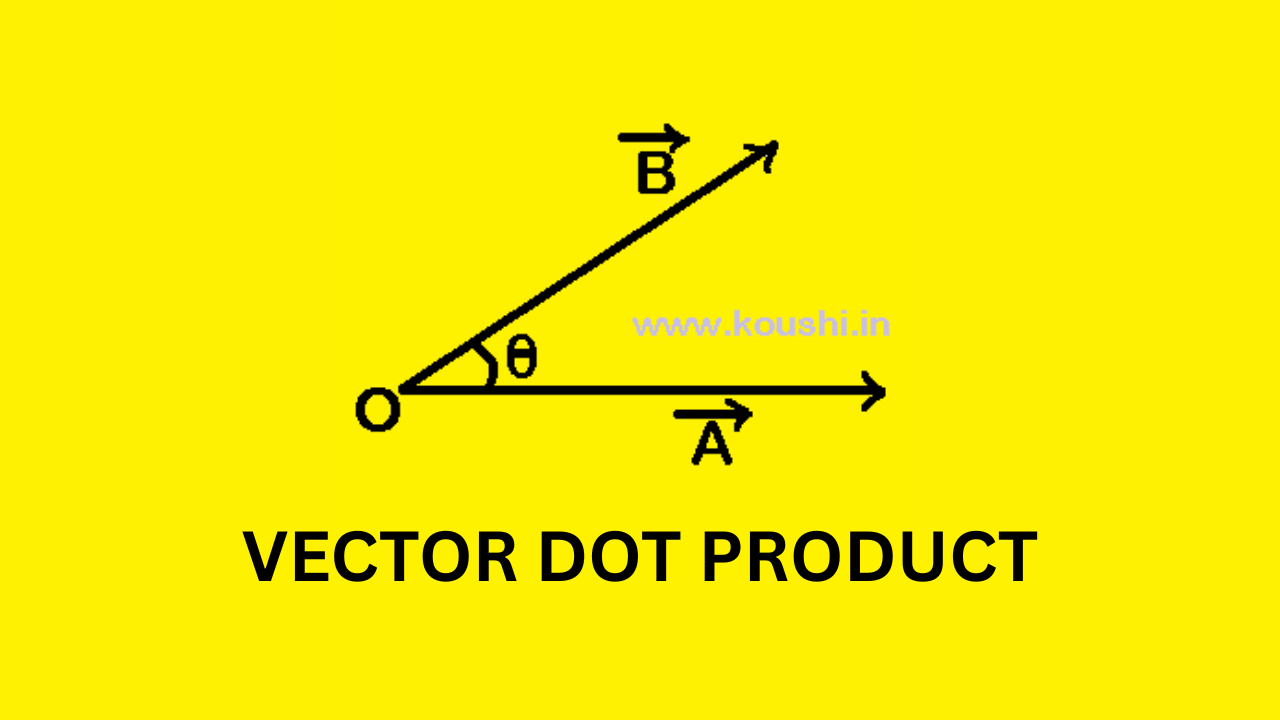
Vector cross product is used to calculate area of triangle, rectangle or parallelogram. We can calculate moment of force or torque using cross product of vector. Vector product or cross product: The vector product of two vectors and is defined as the product of the magnitudes of and and the sine of the angle between […]
Explore More
Vector dot product or scalar product: The dot or scalar product of two vectors and is defined as the product of the magnitudes of and and the cosine of the angle between them. If A and B creates angle θ then, . = AB . Properties of dot product: (i) . = BA = AB […]
Explore More
We can use 3D representation of a vector to calculate position vector of a point. Angle of vector with given axis can be calculated by 3D representation of vector also. Representation of a vector by coordinates: Let us consider, OX, OY and OZ are three perpendicular axes, where O is the origin. Let P is […]
Explore More
Resolution of a vector into its components is the process to determining a set of vectors, whose resultant is the given vector. Each vector in that set is called a component of the given vector. Prove: Let us consider, (= ) is resoluted along the line OA and OB creates angles and respectively. From point […]
Explore More
Vector addition and subtraction problems can be solved by triangle and parallelogram law. Triangle law of vector addition: Statement: If two vectors are represented both in magnitude and direction by two sides of a triangle taken in the same order, then the resultant of these vectors is represented both in magnitude and direction by the […]
Explore More
Vector can be classified in various types. Such types are given below. 1. Polar vectors: The vector which has an initial point or a point of application is known as polar vector. Example: displacement, force etc. Axial vector: The vector which represents the rotational effect and act along the axis of rotation in accordance with […]
Explore MoreBending of a cycle: When a cyclist moves on a curved road of radius r with sped v, he bends slightly at angle θ from his vertical position towards the inner side of the curve. m is the combined mass of the cycle and cyclist. The reaction force (R) offered by the road makes angle […]
Explore MoreDefects of vision of human eye: The most distant point which an eye can see clearly is called the far point (F). For the normal eye the far point lies at infinity. The nearest point which an eye can see clearly is called the near point (N). For normal eye, near point lies at a […]
Explore MoreHuman eye is spherical in shape with a slight bulge at the front. Sclera: The outer part of eye is called sclera. It is white in colour with fibrous layer. The transparent part of it at the front of the outer side of the eye is called cornea. Light enters the eye through it. Its refractive index is […]
Explore MoreFriction due to relative velocity: A block A of mass M is placed on horizontal table. Another block B of mass m is places on block A as shown in figure. Now v1 and v2 (v1 < v2) are the velocities of A and B respectively. The conditions are explained below.1. The coefficient of static […]
Explore More
© 2018 – 2025 Koushi All Rights Reserved