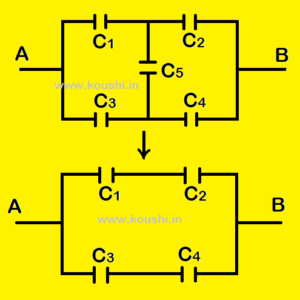
6. Wheatstone bride combination: Calculate equivalent capacitance between points A and B.
If the ratio of capacitors C1 and C2 is same to the ratio of capacitors C3 and C4 then no charge pass through capacitor C5. So, the capacitors C1, C2 and C3, C4 are in series connection and their combinations are in parallel connection between points A and B.
If C1 = C2 = C3 = C4 = C then Ceq = C.
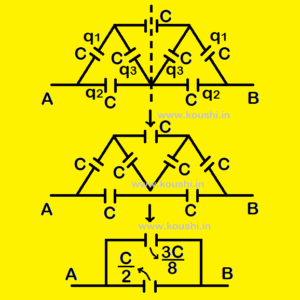
7. Mirror symmetry concept: Calculate equivalent capacitance between points A and B.
In this method capacitors are divided in object and image by considering a mirror on a particular axis (dotted line). The charge of object capacitors are same as that of image capacitors respectively. As the charge of a particular object capacitor is not transfer to other image capacitors, so we can remove the connection of capacitors of charge q3 from point O. Then net capacitance between points A and B of the combination is C’ = ![]() +
+ ![]() =
= ![]() .
.
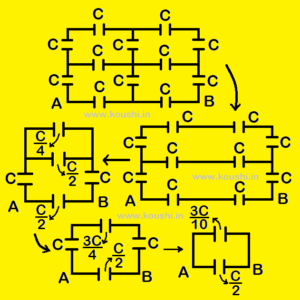
8. Symmetry for same potential: Calculate equivalent capacitance between points A and B. If for a combination AB is the line of symmetry, then all the points lying on perpendicular drawn to AB are of same potential. So, the capacitors in between these points have no charge.
If AB is not the line of symmetry but if it’s perpendicular bisector is line of symmetry then all the points lying on perpendicular are of same potential. So, the capacitors in between these points have no charge.
The capacitance of series combination in between A and B is ![]() .
.
Then net capacitance between points A and B of the combination is C’ = ![]() +
+ ![]() =
= ![]() =
= ![]() .
.
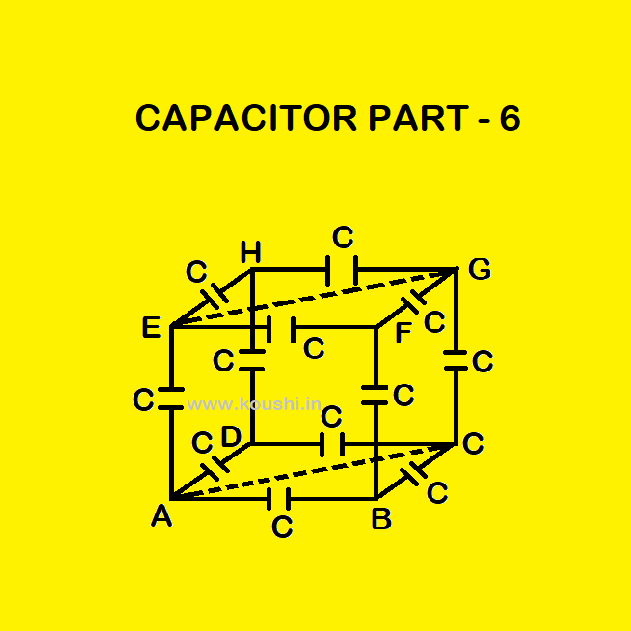
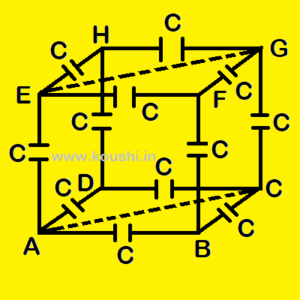
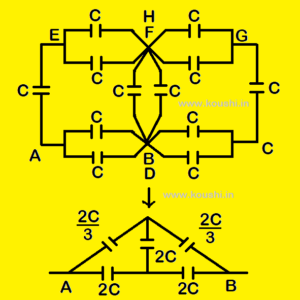
9. Plane of symmetry concept: Calculate equivalent capacitance between points A and C. For three dimensional case of combinations, plane of symmetry involving A and C is to be considered. For the plane ACGE, D and B are symmetrical points, so they are of same potential. Similarly point F and H are also have same potential. Now arrange the capacitors among those points. The combination is like a wheatstone bridge circuit.
Then net capacitance between points A and B of the combination is C’ = ![]() + C =
+ C = ![]() .
.
Click the button to go to the next part of this chapter.
Click the button to go the previous part of this chapter.