Moment Of Inertia Part 1

By Admin Koushi
(0) comments
June 1, 2025

Moment Of Inertia Part 1

Moment of inertia:

According to Newton’s first law of motion, if there is no external force is applied on a body, the body continuous in its state of rest or of uniform motion in a straight line. The property of the body by virtue of which it tends to resist the change its state of rest or of uniform motion in a straight line by itself is known as inertia. For translatory motion, the value of inertia depends only the mass of the body. The greater is the mass greater is the inertia. Kinetic energy in translational motion also depends upon the mass and the linear velocity of the body. But when a body rotates about an axis, the kinetic energy of the rotation is determined not only by its mass and angular velocity but also depends upon the position of the axis about which the body is rotated and the distribution of mass about that axis.

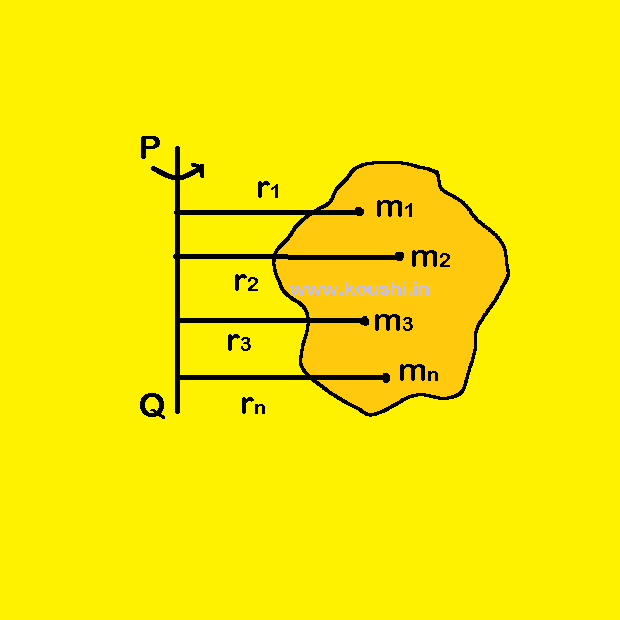
If a body is rotated about an axis PQ with an angular velocity , all the particles have the same angular velocity but the linear velocities are different due to the different distance from the axis of rotation.

Let us consider, the linear velocities of the particles of mass m₁, m₂, m₃ —– , distance r₁, r₂, r₃ —– are respectively v₁, v₂, v₃ —— from the axis of rotation PQ.

The kinetic energy of the body is the sum of the kinetic energies of the various particles and it is given by K.E. = m₁v₁² + m₂v₂²+ ——-

Since v = r, then the K.E. = + ——-

K.E. = (mr² ) = I.

Where I is the moment of inertia of the body about the axis PQ and it is equal to mr².

The moment of inertia of a body about an axis is defined as a sum of the products of the mass and the square of the distance of the different particles of a body from the axis of rotation.

The moment of inertia may also be defined as the twice the kinetic energy of a rotating body when its angular velocity is unity.

Radius of gyration:

If the total mass of the body is supposed to be concentrated at a point such that the kinetic energy of rotation of that point is the same as that of the body itself then the distance of that point from the axis of rotation is called radius of gyration of the body about that axis.

K.E. = I = (mr² )= M

Therefore, Mk² = mr² = mn()

Where n is the number of particles each of mass m into which the given mass M is divided.

Therefore, k =

Hence the radius of gyration is the square root of the mean square distance of the particles of the body from the axis of rotation.

Physical significance of moment of inertia:

Moment of inertia plays the same role in rotatory motion as a mass does in linear motion. So, moment of inertia is an analogue of mass in linear motion.

According to Newton’s first law if there is no external force is applied on a body, the body continues in its state of rest or of uniform motion in a straight line. This property is known as inertia. A body always resists the external force tending to change its state of rest or of linear motion. Therefore, for the body of greater mass, greater force is required to produce a given linear acceleration.

Similarly, bodies process rotational inertia. When a body is free to rotate about an axis, it opposes any change in its state of rest or of rotation. Greater the moment of inertia of a body greater is the couple required to produce a given angular acceleration. The moment of inertia depends not only on the mass of a body but also on the distribution of mass about the axis of rotation.

Perpendicular axis theorem for moment of inertia:

The moment of inertia of a uniform plane lamina about an axis passing perpendicular to its plane is equal to the sum of its moment of inertia about any two mutually perpendicular axes in this plane intersecting on the first axis.

Let us consider OZ be the axis perpendicular to the plane of the lamina about which the moment of inertia is to be measured.

Let OX and OY be two mutually perpendicular axis on the plane of the lamina and intersecting on OZ.

Let us consider a particle P of mass m is at a distance r from OZ on XY plane.

The moment of inertia of the particle about OZ is mr².

Therefore, the moment of inertia of the entire lamina about OZ is I_Z =∑mr².

From diagram r² = x² + y²where x and y are the distance of P from OY and OX axes respectively.

Here moment of inertia of the lamina about OX is I_X =∑my² and that of about OY is I_Y =∑mx².

Therefore, I_Z = ∑mr² =∑m (x² + y²) = I_Y + I_X

∴ I_Z = I_X + I_Y.

Parallel axis theorem of the moment of inertia:

The moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis passing through its centre of mass plus the product of the mass of the body and the square of the perpendicular distance between the two axes.

Let us consider I be the moment of inertia about an axis AB of a plane lamina. I_g is the moment of inertia about a parallel axis EF passing through the centre of mass (point C) of the lamina. The distance between AB and EF is h.

Let us consider a particle P of mass m is at a distance r from EF.

Its moment of inertia about AB is m(h + r)².

Therefore, the moment of inertia of the entire lamina about AB is given by I =

Parallel axis theorem of the moment of inertia:

Let us consider I be the moment of inertia about an axis ABof a plane lamina. I_g is the moment of inertia about a parallel axis EF passing through the centre of mass (point C) of the lamina. The distance between AB and EF is h.

Let us consider a particle P of mass m is at a distance r from EF.

Its moment of inertia about AB is m(h + r)².

Therefore, the moment of inertia of the entire lamina about AB is given by I =Σm (h + r)²

Or, I =Σm (h² + 2hr + r²)

Or, I = Σmh² + Σm2hr +Σm r²

Since h is constant, it can be put outside of Σ

∴ I = h²Σm+ hΣm2r +Σm r²

Here Σm r² = I_gis the moment of inertia of the lamina about its centre of mass.

h^2Σm = Mh² where M is the total mass of the lamina.

Σm2r = 0 because the sum of the moment of all the particles of a body about an axis through the centre of mass of the body is zero as the body is balanced about the centre of mass.

Therefore, the moment of inertia of the entire lamina about AB is given by I = I_g + Mh².

Moment of inertia of a uniform rod:

Moment of inertia of a uniform rod about an axis passing perpendicularly through its one end:

Let us consider a rod of mass M and length L is rotated about an axis passing perpendicularly through its one end.

Mass per unit length of the rod is dm =

We consider an elementary part of the rod at a distance x of thickness dx.Mass of that elementary part is dm = dx

Moment of inertia of that elementary partabout that axisis dI = dmx² = x²dx

Therefore, the moment of inertia of the entire rod about that axis is I = = dx = = .

Moment of inertia of a uniform rod about an axis passing through its centre perpendicularly:

Let us consider a rod of mass M and length L is rotated about an axis passing perpendicularly through its one end.

We consider the axis of rotation passes through the origin lying on Y axis and the x coordinates of two ends of the rod are respectively (+,- ).Mass per unit length of the rod is dm =

We consider an elementary part of the rod at a distance x of thickness dx.Mass of that elementary part is dm = dx

Moment of inertia of that elementary part about that axis is dI = dmx² = x²dx

Therefore, the moment of inertia of the entirod about that axis is I = = x²dx = = [+= ]=

Moment of inertia of a thin rectangular lamina:

Let us consider a thin uniform rectangular lamina of length L, breadth b and mass M.The following cases may arise.

Moment of inertia of a rectangular lamina about an axis passing through its edge lying on its plane parallel to its length.

The entire lamina can be assumed to be made up of a large number of thinstrips parallel to its breadth with mass dm and length b.

Any one strip is rotated about the axis passing through its one endperpendicularly.

The moment of inertia of that strip is dI = .

The moment of inertia of the entire lamina about that axis is I = = = .

Moment of inertia of a rectangular lamina about an axis passing through its edge lying on its plane parallel to its breadth.

The entire lamina can be assumed to be made up of a large number of thin strips parallel to its length with mass dm and length L.

Any one strip is rotated about the axis passing through its one end perpendicularly.

The moment of inertia of that strip is dI = .

The moment of inertia of the entire lamina about that axis is I = = = .

Moment of inertia of a rectangular lamina about an axis passing through its centre perpendicular to its length.

The entire lamina can be assumed to be made up of a large number of thin strips parallel to its length with mass dm and length L.

Any one strip is rotated about the axis passing through its centre perpendicularly.

The moment of inertia of that strip is dI = .

The moment of inertia of the entire lamina about that axis is I = = = .

Moment of inertia of a rectangular lamina about an axis passing through its centre perpendicular to its breadth.

The entire lamina can be assumed to be made up of a large number of thin strips parallel to its breadth with mass dm and length b.

Any one strip is rotated about the axis passing through its centre perpendicularly.

The moment of inertia of that strip is dI = .

The moment of inertia of the entire lamina about that axis is I = = = .

Moment of inertia of a rectangular lamina about an axis passing through its centre perpendicular to its plane.

Let us consider X, Y and Z are three mutually perpendicular axis where origin is at the centre of the lamina.

The moment of inertia of the lamina about the axes X and Y are respectively I_X = , I_Y = .

The moment of inertia of the lamina about the axis passing through its centre perpendicularly is I_Z = I_X+ I_Y [using perpendicular axis theorem].

∴I = I_Z = + = [L² + b²].

Moment of inertia of a rectangular lamina about an axis passing through its any corner and perpendicular to its plane.

We consider a parallel axis with respect to the axis of rotation through the centre of the lamina.

Moment of inertia of that axis passing through the centre of lamina perpendicular to its plane is I_g = [L² + b²].

Using parallel axis theorem we get, I = Ig + Mh²

where h² = ()² + ()² = [L² + b²].

Or, I = [L² + b²] + [L² + b²]

∴ I = [L² + b²].

Moment of inertia of rectangular lamina about its any diameter.

Two diameters of rectangular lamina intersect perpendicularly at its centre. As the body is symmetrical about its diameter, therefore, moment of inertia about twodiametersare equal in magnitude.

If we consider an axis passing through the centre of the laminaperpendicularly, then these three axes of rotation are mutually perpendicular.

Hence, we can use perpendicular axis theorem, I_Z = I_X + I_Y

Or, [L² + b²] = I + I

∴I = [L² + b²].

Moment of inertia of uniform bar of rectangular cross section:

Let us consider a uniform bar of length L, breadth b and thickness t.Mass of the bar is M.

Moment of inertia of a solid uniform bar of rectangular cross section about an axis perpendicular to its length and passing through the centre of gravity.

Let us consider PQ is the axis of rotation passing through its centre and perpendicular to its length.

We can imagine the whole bar to be divided into a large number of thin rectangular sheets (lamina) at right angle to the thickness of the bar with mass dm.

The moment of inertia of that elementary sheet about PQ is dI = [L² + b²].

Therefore, the moment of inertia of the whole bar about PQ is the sum of moment of inertia of all such sheets.

So, I = = [L² + b²] = [L² + b²].

In case of cube, L = b = a and I = .

Moment of inertia of a solid uniform bar of rectangular cross section about an axis perpendicular to its length and passing through one of the corners.

To calculate moment of inertia about P^/Q^/, we can use parallel axis theorem with the distance between PQ and P^/Q^/ is d.

Therefore, moment of inertia about P^/Q^/ is I = I_PQ + Md²

∴I = [L² + b²] + [L² + b²] = [L² + b²].

In case of cube, L = b = a and I = .

Moment of inertia of a triangular lamina:

Let us consider a triangle of base b, height h and mass M. The area of the triangle is .Mass per unit area of the triangle is = .

Moment of inertia of a triangular lamina about one side of the triangle as axis.

Let us consider the triangle is rotated about the base QR.We consider and elementary strip AB of thickness dx at a distance x from QR.As the Δ PAB and ΔPQR are similar, then we can write =

Or, AB =

The area of the elementary strip is ABdx

Mass of the elementary strip is dm = ABdx = × =

Moment of inertia of elementary strip about the axis QR is dI = dmx².

Moment of inertia of the entire triangle about the axis QR is

I = =

Or, I = ()dx

∴ I = [h. – ] = .

Moment of inertia about an axis passing through the centre of gravity of the triangle and parallel to one of its sides.

Let us considered G is a centre of gravity of the ΔPQR and the axis FGH is parallel to the side QR.

It is required to calculate the moment of inertia of ΔPQR about this axis.

Using parallel axis theorem we have, moment of inertia of the ΔPQR about QR = moment of inertia of the ΔPQR about FGH + mass of the triangular lamina × ()².

Therefore, moment of inertia of the ΔPQR about FGH = moment of inertia of the ΔPQR about QR – mass of ΔPQR × ()²

∴ moment of inertia of the ΔPQR about FGH = – = .

Moment of inertia of the triangle about an axis passing through the vertex P and parallel to QR.

Applying parallel axis theorem we get, moment of inertia of ∆PQR about the axis APB = moment of inertia of ∆PQR about the axis FGH + mass of ∆PQR × ()2.

∴ moment of inertia of the ∆PQR about APB = + = .

Moment of inertia of a uniform ring:

Let us consider a uniform ring of mass M and radius R is rotated.

Moment of inertia of a ring about an axis passing through its centre perpendicular to its plane.

We consider an elementary part of the ring of mass dm is rotated about that axis with radius R.

The moment of inertia of the elementary part about that axis is dI = dmR2

The moment of inertia of the entire ring about that axis is I = ∫dI = ∫dm = M.

Moment of inertia of the ring about an axis passing through its any diameter.

Let us consider X, Y and Z are three mutually perpendicular axes and the origin is at the centre of the ring.

We consider two axes of rotation about the diameter which passes through X and Y axes respectively. As the ring is symmetrical about diameter, therefore, the moment of inertia about X and Y axes remain same.

Using perpendicular axis theorem we get, IZ = IX + IY

Or, M = I + I [ is the moment of inertia of the ring passing through its centre]

∴ I = .

Moment of inertia of a uniform ring about an axis passing through its edge and perpendicular to its plane.

We consider PQ is the access passing through the edge of the ring and perpendicular to its plane. P/Q/ is the axis which is perpendicular to the plane of the ring passing through its centre. Using parallel axis theorem we get, = + M

Or, I = M + M [∵ h = R]

∴ I = 2M.

Moment of inertia of a uniform ring about an axis passing through its edge lying on its plane.

Let us consider PQ is the axis passing through the edge of the ring lying on its plane. P/Q/ is the axis parallel to PQ along diameter.

Using parallel axis theorem we get, = + M

Or, I = + M[∵ h = R]

∴ I =

Moment of inertia of a uniform disc:

Let us consider a uniform disc of mass M and radius R is rotated. The mass per unit area of the disc is = MπR2.

Moment of inertia of a disc about an axis passing through its centre perpendicular to its plane.

We consider an elementary ring of radius r with thickness dr about that axis. The area of that elementary ring is dA = 2rdr. Mass of that elementary ring is dm = 2πrdr = .

The moment of inertia of the elementary ring about that axis is dI = dm = .

The moment of inertia of the entire disc about that axis is I = ∫dI = = =

∴ I =

Moment of inertia of the disc about an axis passing through its any diameter.

Let us consider X, Y and Z are three mutually perpendicular axes and the origin is at the centre of the disc.

We consider two axes of rotation about the diameter which passes through X and Y axes respectively. As the disc is symmetrical about diameter, therefore, the moment of inertia about X and Y axes remain same. Using perpendicular axis theorem we get, = +

Or, = I + I [IZ is the moment of inertia of the disc passing through its centre]

∴ I = .

Moment of inertia of a uniform disc about an axis passing through its edge and perpendicular to its plane.

We consider PQ is the access passing through the edge of the disc and perpendicular to its plane. P/Q/ is the axis which is perpendicular to the plane of the disc passing through its centre. Using parallel axis theorem we get, = Ig +M

Or, I = + M [∵ h = R]

∴ I = .

Moment of inertia of a uniform disc about an axis passing through its edge lying on its plane.

Let us consider PQ is the axis passing through the edge of the disc lying on its plane. P/Q/ is the axis parallel to PQ along diameter.

Using parallel axis theorem we get, = Ig + M

Or, I = + M[∵ h = R]

∴ I = .

Moment of inertia of a uniform rigid circular cylinder:
Moment of inertia of a uniform rigid circular cylinder about its own axis.

Let us consider a uniform cylinder of mass M, radius R and length L is rotated about its own axis PQ.

We can consider the entire cylinder consists of a large number of elementary discs of negligible thickness with mass dm and radius R.

Moment of inertia of each elementary disc about axis PQ is dI =

Therefore, the moment of inertia of the entire cylinder about its own axis is I = = .

Moment of inertia of a uniform rigid circular cylinder about an axis passing through its centre and perpendicular to its geometrical axis.

Let us consider O is the centre of mass of the cylinder of length L, radius r and mass M.

If is the density of the material of the cylinder then, ρ = .

Let us consider OX is the geometrical axis of the cylinder and OY is the axis of rotation which is perpendicular to OX.

The cylinder may be taken as made up of a number of discs of radius R with their plane parallel to OY.

Let us considered an elementary disc at a distance x from O with thickness dx.

The volume of the disc is dv = dx

The mass of that elementary disc is dm = ρdx = = .

Let us consider PQ is the axis which is parallel to OY and passing through the centre of that elementary disc.

The moment of inertia of that elementary disc about the axis PQ [along the diameter] is Ig = = .

The moment of inertia of the elementary disc about OY is dI = Ig + dm [using parallel axis theorem]

Or, dI = +

The moment of inertia of the entire cylinder about the axis OY is I = ∫dI = [ + ]dx

Or, I = 2×

Or, I = 2 ×[ +

∴ I = M[+ ].

Moment of inertia of a right circular solid cone:
1.About its axis of symmetry.

Let us consider, a uniform right circular solid cone of mass M height h and radius of base is R is rotated about its axis of symmetry PQ.

The volume of the cone is .

If is the density of the material of the cone then, = .

The cone is supposed to be made up of a large number of coaxial circular disc parallel to the base.

We consider one such elementary circular disc of radius r and thickness dx at a distance x from vertex of the cone.

From diagram, tan = =

Or, r =

The volume of the elementary disc is dv = πdx =

Mass of that elementary disc is dm = dv = =

The moment of inertia of that elementary disc about the axis PQ [passing through its centre perpendicular to its plane] is dI = = =

Moment of inertia of the entire cone about the axis PQ is I = dI = = = .

Moment of inertia of a uniform right circular solid cone about an axis passing through its vertex and parallel to its base.

Let us consider, a uniform right circular solid cone of mass M height h and radius of base is R is rotated about an axis PQ passing through its vertex A parallel to its base.

The volume of the cone is .

If is the density of the material of the cone then, = .

The cone is supposed to be made up of a large number of coaxial circular disc parallel to the base.

We consider one such elementary circular disc of radius r and thickness dx at a distance x from vertex of the cone.

From diagram, tan = =

Or, r =

The volume of the elementary disc is dv = =

Mass of that elementary disc is dm = dv = =

Let us consider P/Q/ is the axis passing along the diameter of the elementary disc parallel to PQ.

The moment of inertia of that elementary disc about the axis PQ [using parallel axis theorem] is dI = Ig + dm = moment of inertia of that elementary disc about the axis P/Q/ + dm = + dm

Or, dI = + = +

The moment of inertia of the entire cone about the axis PQ is I = ∫dI = [ + ]dx

Or, I =

Or, I = [ + ]

∴ I = [ + ].

Moment of inertia of a spherical shell:

Moment of inertia of a spherical shell about an axis passing through its diameter.

Let us consider, a thin spherical shell of mass M and radius R is rotated about an axis (OX) passing through its diameter.

The mass per unit area of the shell is = .

Let us consider a thin element of shell lying between two planes AB and CD perpendicular to OX at a distance x and (x + dx) from O. This is a circular ring of width AC = Rd [Let ∠YOA = and ∠AOC = dθ] and radius y.