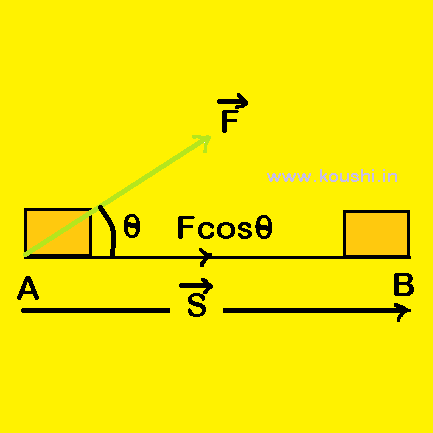
Work: Work is said to be done when a force is applied on a body and the body is displaced through a certain distance in the direction of the applied force.
If F is the force is applied on a body at an angle θ with displacement S, then work done on the body is W = Fcos
S = 
.
Unit: SI unit of work is joule (J) = 1newton
1meter
C.G.S. unit of work is erg = 1dyne1centimeter
1J = 105dyne102cm = 107erg.
Dimension of work [W] = [F][S] = [MLT-2][L] = [ML2 T-2].
Click the button given to learn about the following topics:
- Positive work done, negative work done, zero work
- Concepts on work done against friction
- Work done by the pair of interactive force
- Graphical representation of work
Kinetic energy: The energy possessed by a body by virtue of its motion is called kinetic energy.
Let us consider a body of mass m is initially at rest. It is applied by an external force F and the velocity of the body is v after travelling a distance s. The acceleration of the body is a = 
.
Then v2 = 2as
Or, v2 = 
Or, Fs = 
Or, W = K.E. of the body.
Click the button given to learn about the following topics:
- Work energy theorem
- Work done by pseudo force.
Concepts on energy:
1. A ball is moving with speed v and after striking by bat the ball is moved with speed 1.5v in opposite direction. Find the change in momentum of the ball if the change in kinetic energy is E.
Let us consider the mas of the ball is m. The change in kinetic energy is E = 
– = 
Or, m = 
.
Therefore, change in momentum of the ball = m[1.5v – (-v)] = 2.5mv = 
= 
.
2. A body of mass m is initially at rest. F force is applied on it for time t. Find the kinetic energy of the body at time t.
The acceleration of the body is a = . The speed of the body at time t becomes v = at = 
.
The kinetic energy of the body at time t is E = = 
= 
.
Kinetic energy due to explosion: Let us consider a body is initially at rest. Due to explosion the body is divided into two parts. One part of mass m is moving with speed u and the other part of mass M (M>m) is moving with speed v in opposite direction. The kinetic energy of masses m and M is Em and EM respectively.
Therefore, 
= 
= 
.
Using conservation of linear momentum, we get, mu = Mv or, u = 
.
So, = 
= 
.
Therefore, kinetic energy is inversely proportional of mass. As M>m, so, Em > EM.
If the total kinetic energy is E, then E = Em + EM = 
+ 
Or, E = 
Or, E = 
Or, E = 
Or, E = 
Or, EM = 
Similarly, Em = 
.
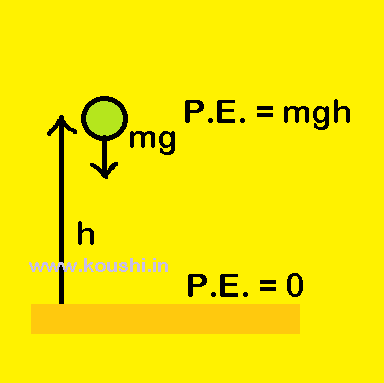
Potential energy: The energy possesses by a body by virtue of its position or configuration (shape) is called potential energy.
Let us consider a body of mass m is placed at a height h against h against gravity.
The potential energy = work done =force displacement = mgh.
Concept on potential energy: A body of mass m is freely falling under gravity. Find the loss of potential energy of the body at tth second of its motion.
Let us consider the body travels distance x for time t then, x = 
The distance travelled by the body for (t-1) second is y = 
Distance travelled by the body for tth second is s = x – y = – = 
Therefore, loss of potential energy of the body at tth second of its motion is E = Fs = mgs = 
.
Difference between kinetic energy and Potential energy:
kinetic energy | potential energy |
1. The energy possessed by a body by virtue of its motion. | 1. The energy possess by a body by virtue of its position or configuration. |
2. Kinetic energy of a body of mass m is moving with velocity v is | 2. The potential energy of a body of mass m at a height h from earth’s surface is mgh. |
3. Kinetic energy always positive. | 3. Potential energy can be negative. Example – gravitational potential |
Relation between kinetic energy and momentum of body: Let us consider a body of mass m is moving with velocity v, then the kinetic energy of the body is E = and the momentum of the body is P = mv.
Or, E = 
= 
Or, P = 
.
(1) If two bodies of same mass moving with kinetic energy E1 and E2 then the ratio of momentum P1 : P2 = 
.
(2) If two bodies are moving with same kinetic energy but of different masses m1 and m2 then the ratio of momentum P1 : P2 = 
.
(3) ) If two bodies of masses m1 and m2 are moving with kinetic energy E1 and E2 and momentum of two bodies remain same then, m1: m2 = E2:E1.
Click the button given to learn about the following topics:
- Potential energy stored in spring
- Energy vs elongation graph of spring
- Calculation of force constant for various combinations of spring
Click the button given to learn about the following topics:
- Circular motion of a body in vertical plane
- Concepts on vertical circular motion
Click the button given to learn about the following topics:
- Definition of conservative and non conservative field
- Example of conservative and non conservative field
- Relation between potential energy and conservative force
Click the button given to learn about the following topics:
- Law of conservation of mechanical energy
- Conservation of mechanical energy of a body on smooth inclined plane
- Various applications of law of conservation of mechanical energy
Conservation of energy for freely falling body: Let us consider a body of mass m is placed at point A, at a height h from earth’s surface.
Potential energy at point A is P.E. = mgh
As the body is rest at A, then velocity at point A is 0. So, kinetic energy at point A is K.E. = 0
Total energy of body at point A is T.E. = P.E. + K.E. = mgh + 0 = mgh
Now the body is freely falling under gravity and at any instant it is at point B, at a height x from ground.
Potential energy at point B is P.E. = mgx [height = x]
Velocity of body at point B is vB then, vB2 = u2 + 2as = 2g(h-x) [as u = 0, a = g and displacement of body is (h –x)]
Kinetic energy of body at point B is K.E. = 
mvB2 = m2g(h-x) = mg(h-x)
Total energy of body at point B is T.E. = P.E. + K.E. = mgx + mg(h-x) = mgh
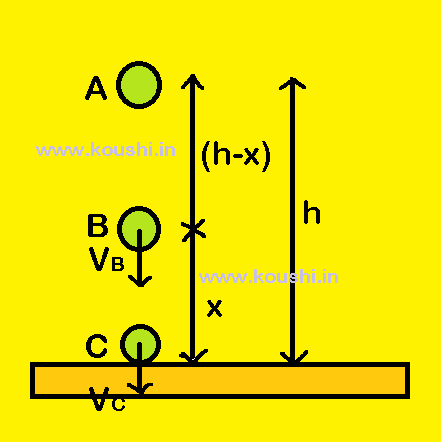
Now the body is at point C, just before touching the ground. So, height from ground is 0.
Potential energy at point C is P.E. = 0 [height = 0]
Velocity of body at point C is vC then, vC2 = u2 + 2as = 2gh [as u = 0, a = g and displacement of body from A is h]
Kinetic energy of body at point C is K.E. = mvC2 = m2gh = mgh
Total energy of body at point C is T.E. = P.E. + K.E. = 0 + mgx = mgh
Therefore total energy remain same at all points on the freely falling motion of a body. So, mechanical energy is conserved.
Click the button given to learn about the following topics:
- Definition of power
- Unit and dimension of power
- Various conceptes of power
Electrical power: Electric power is defined as the amount of electrical energy consumed in a circuit per unit time. If W is the amount of electrical energy consumed in a circuit for time t, then electrical power P = 
= 
= VI. [V = potential difference, I = current]
Electric power is defined as the product of the potential difference across the circuit and current flowing through it.
Commercial unit of current: A kilowatt-hour is the amount of electric energy consumed by 1000 watt electric appliance when it is operated for 1 hour.
1BOT = 1 kilowatt-hour =1000Wh = 10003600 Ws = 3.6106 J.