Potential energy of spring: When a spring is compressed or elongated by a force F and the elongation or compression is x, then F 
x.
Or, F = kx [where k is the force constant of spring] ——-(i)
If Fe is the elastic force or restoring force applied by spring, then Fe = – kx [Fe is always towards the mean position].
Now the spring is further stretched through a distance dx, therefore the work done by the spring for further stretching is dw = -Fe.dx = Fedxcos1800 = -Fedx = -kxdx [using equation (i)]
Therefore the work done to stretched the spring through a distance x from its normal position(x = 0) is
W = 
dW = –
kxdx = -k[
] = – 
kx2 = potential energy of spring.
If spring is elongated from xi to xf, then work done by spring is w = – k(
– 
).
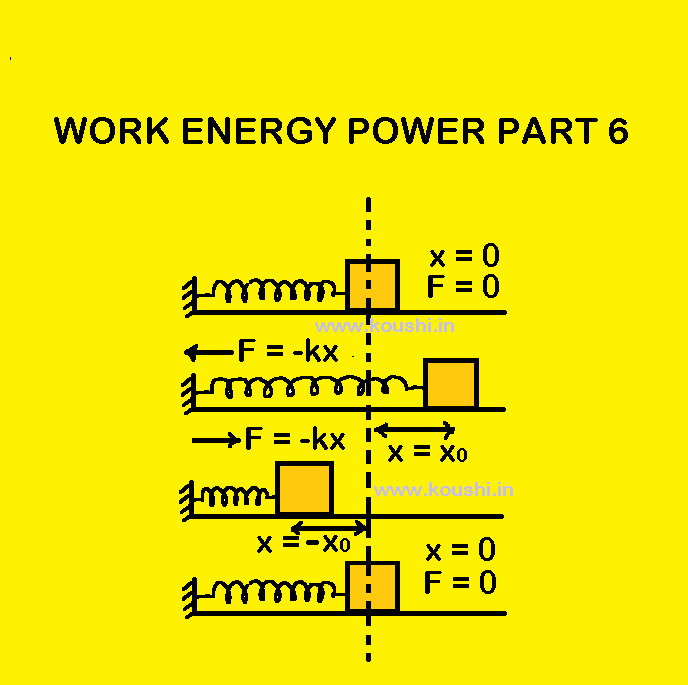
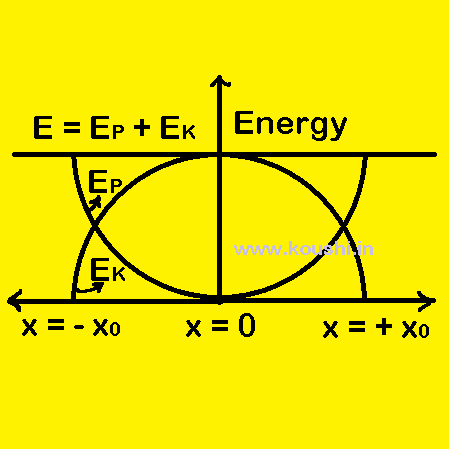
Conservation of energy of spring: When a spring is at unstretched condition, the potential energy of the spring is zero. Now F force is applied and the elongation of it is x and the potential energy of spring is kx2. At this time spring is at extreme position. Now the spring moves to its normal position due to elastic property, and at that condition total energy is kinetic energy i.e. kx2. When the spring is in extreme compressed position again total energy is converted to potential i.e. kx2 and this process continues. So energy is conserved in vibrating spring.
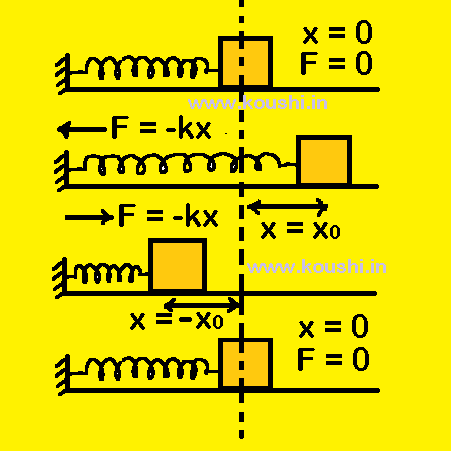
Force constant of spring calculation:
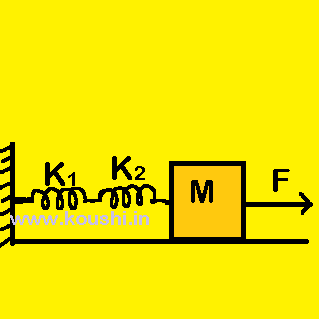
1. Spring in series: Two massless springs of force constant k1 and k2 are connected in series as shown in figure. Due to applied force F on the body the body is displaced by x. As the springs are massless, so the force acts on each spring is also F. If x1 and x2 are the elongation of two springs of force constant k1 and k2 respectively, then
F = k1x1 and F = k2x2.
But x1 + x2 = x. So, 
+ 
= x
If k is the equivalent force constant [replacing two springs by a single spring keeping force and elongation same] then, + = 
Therefore, in series connection of spring 
= 
+ 
.
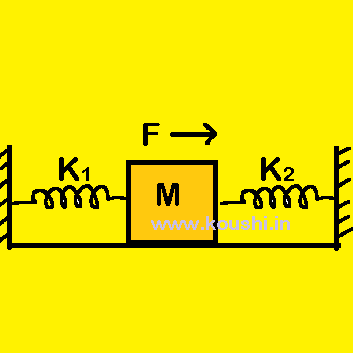
2. Spring in parallel: (i) Two massless springs of force constant k1 and k2 are connected in parallel as shown in figure. Due to applied force F, the body is displaced by x.
Therefore, the elongation of each spring is also x.
If F1 and F2 are the force applied on two springs of force constant k1 and k2 respectively, then F1 = k1x and F2 = k2x.
Here F = F1 + F2 = k1x + k2x = (k1 + k2)x
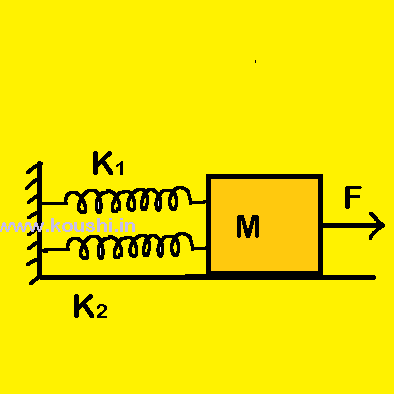
If k is the equivalent force constant [replacing two spring by a single spring keeping force and elongation same] then, kx = (k1 + k2)x. Therefore, in parallel connection of spring k = k1 + k2.
(ii) In this figure when F force is applied on body towards right to displaced it by x, then spring k1 is expanded by x where F1 is the spring force produced. Similarly, spring k2 is compressed by x where F2 is the spring force.
Therefore, F = F1 + F2 = k1x + k2x = (k1 + k2)x
If k is the equivalent force constant [replacing two spring by a single spring keeping force and elongation same] then, kx = (k1 + k2)x
Therefore, the equivalent force constant k = k1 + k2.
