Laws of conservation of mechanical energy: It state that the total mechanical energy of a system remain constant if only conservative forces are acting on the system of particles and the work done by all other forces is zero.
The initial potential and kinetic energy of the system are Ui and Ki respectively. The final potential and kinetic energy of the system are Uf and Kf respectively.
For conservative force the change in potential energy is equal to negative work done. So, – W = Uf – Ui
From work energy theorem, the work done on the system is the change in kinetic energy. So, W = Kf – Ki
Therefore, Ui – Uf = Kf – Ki
 Ui + Ki = Uf + Kf
Therefore, in conservative field, total mechanical energy is conserved.
When non conservative forces like friction are acting on the system then total mechanical energy is not constant but work energy theorem is valid.
If conservative, non-conservative and external forces are acting on the system, then using work energy theorem we get, WC + WNC + Wext = Kf – Ki
But, – WC = Uf – Ui
So, WNC + Wext = Kf – Ki + Uf – Ui
Or, WNC + Wext = Kf + Uf – (Ki + Ui) = Ef – Ei = change in mechanical energy
Therefore, when work is done by the forces other than conservative forces (like non conservative and external), then it is equal to the change in mechanical energy.
Click the button given to get the derivation of conservation of mechanical energy for freely falling body
Conservation of mechanical energy on smooth inclined plane: Let us consider a body of mass m is placed at point A on an inclined plane at height h from ground. The angle of inclination is 
.
The potential energy at point A is P.E. = mgh
As the body is initially at rest at that point, then the kinetic energy at point A is K.E. = 0.
The total energy at point A is T.E. = mgh
Now the body is moving downward along the inclination with acceleration a = gsin. During its downward motion the body is at point D and the speed of the body at that point is v. DE is perpendicular on AC. The vertical downward displacement of the body at point D is AE = x.
The potential energy at point D is P.E. = mg(h – x)
Using the equation of motion v2 = u2 + 2as we get, v2 = 0 + 2gsinAD = 2gsin
 = 2gAE = 2gx.
The kinetic energy at point D is K.E. = 
 = 
 = mgx
The total energy at point D is T.E. = mg(h – x) + mgx = mgh.
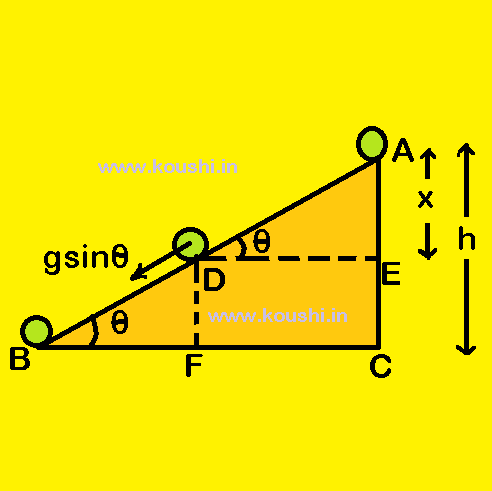
Let us consider the speed of the body before touching the ground at point B is v/.
Therefore, 
= 2gsinAB = 2gsin
 = 2gAC = 2gh.
At point B the height of the body from ground is zero. So, potential energy at point B is P.E. = 0
The kinetic energy at point B is K.E. = 
 = 
 = mgh
The total energy at point D is T.E. = mgh
Therefore, the mechanical energy is conserved for a body moving on smooth inclined plane.
1. A body is displaced from point P to point Q. The kinetic energy and the potential energy of the body at point P and Q are given respectively KP = 25 J, UP = -15 J, KQ = 5 J and UQ = 8 J. Find the work done by (i) conservative forces (ii) all forces (iii) forces other than conservative forces.
For conservative force the change in potential energy is equal to negative work done.
So, – WC = UQ – UP = 8 – (-15) = 23 J
 WC = – 23 J.
According to work energy theorem, work done by all forces is equal to change in kinetic energy.
Wall = KQ – KP = 5 – 25 = – 20 J
Work done by forces other than conservative forces is equal to change in mechanical energy
Wother = KQ + UQ – (KP + UP) = (5 + 8) – (25-15) = 13 – 10 = 3 J.
2. A weight less pan is fitted with a vertical spring as shown in figure. A block of mass m strikes the pan after falling through a height h. If the force constant of spring is k, then find the maximum compression of the spring.
Let us consider the maximum compression of the spring is x. Spring force and gravitational forces are conservative then using conservation of mechanical energy we get,
Ksi + Usi + KBi + UBi = Ksf + Usf + KBf + UBf
Or, 0 + 0 + 0 + mgh = 0 + 
 + 0 + (-mgx)
Or, 
 – 2mgx – 2mgh = 0
 x = 
 = 
= 
.
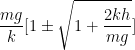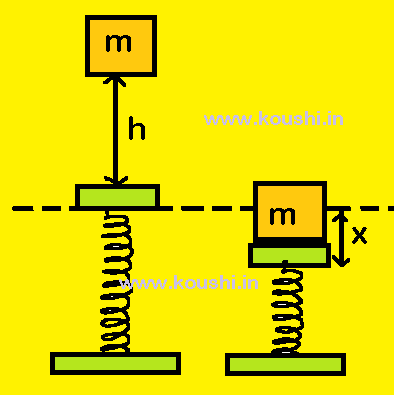
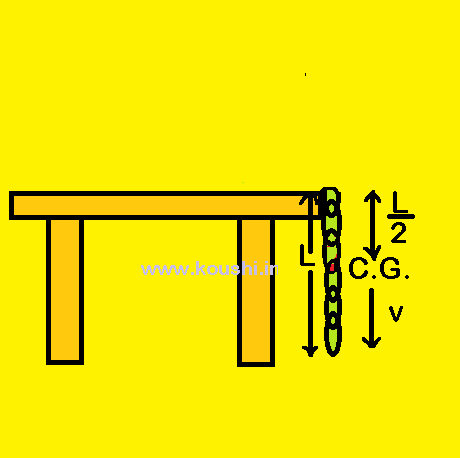
3. A uniform chain of length L mass M is held on a frictionless table with nth (<1) part of its length hanging over the edge. When the chain is released, find the velocity of the chain while leaving the table.
Let us considered the surface of the table as the zero potential or reference level.
Initially the hanging part of the chain is nL. The centre of gravity of the hanging part of chain is at a distance 
 from the reference level.
The initial potential energy of the hanging part of chain is
Ui = -(
nL)g = – 
.
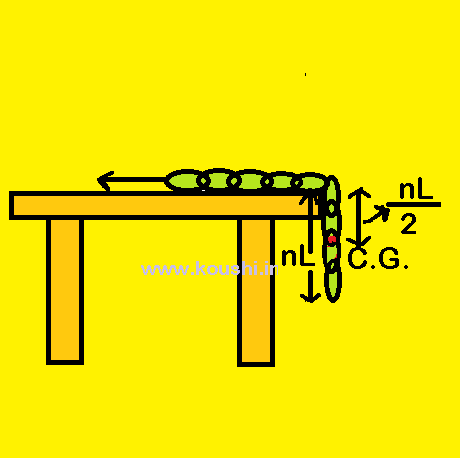
When the end part of the chain leaving the table at that instant the centre of gravity of the chain is at a distance of 
from the reference level.
Therefore, final potential energy of the hanging part of chain is Uf = – 
.
Using conservation of energy we get, Ui + Ki = Uf + Kf
Or, – + 0 = – + 
 v = 
.
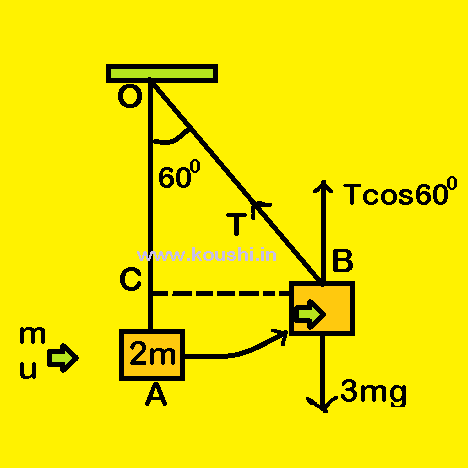
4. A block of mass 2m is suspended by a string of length l from celling. A bullet of mass m is moving horizontally and enters into the block. The block and the bullet move a maximum height. At the maximum height, the string creates angle 600 with vertical. If the string remains stretched at that condition find the tension on the string and the speed of the bullet before entering the block.
Let us consider the block is initially at point A and during maximum height it is at point B. BC is perpendicular on OA.
Therefore the maximum height h = AC = OA – OC = OA – OB cos600 = l(1 – cos600) = 
.
The speed of the block and bullet at point A [after bullet enters into the block] is v.
Using conservation of mechanical energy we get, kinetic energy at point A = potential energy at point B
Or, 
= (m+2m)gh
Â
Or, 
= 
Or, v = 
If the horizontal speed of the bullet before entering the block is u, then using conservation of linear momentum we get, mu + 2m = (m+2m)v
u = 3v = 3.
If T is the tension of the string at point B, then Tcos600 = (m + 2m)g
 T = 6mg.