Circular Motion

By Admin Koushi
(0) comments
June 24, 2025

Circular Motion

Circular motion:

Angular displacement: When a particle is in circular motion about an axis or centre, the angle described by the radius about the axis or centre is called angular displacement.

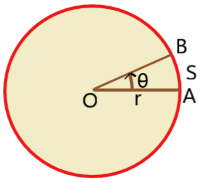
A particle rotates in a circular path of radius r about the centre O.

The particle moves from A to B through the circumference of the circle.

The angular displacement of the particle is = =

SI unit of angular displacement is radian. radian = .

Dimension of angular displacement or dimensionless.

Angular speed: The angular displacement per unit time is called angular speed.

If is the angular displacement for time t then angular speed is [where represents the small change.]

SI unit of angular speed is radian/second or .

Dimension of angular speed is .

Another unit of angular speed is revolution per minute (rpm) = 1rpm = = .

Time period: The time taken by the particle to complete one rotation is called time period.

Frequency: The number of full rotation completed by the particle in one second is called frequency.

So, Frequency = .

Relation between angular speed and time period: Angular speed = .

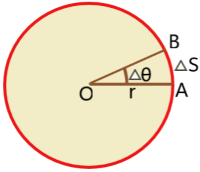
Relation between linear speed and angular speed: A particle rotates in a circular path of radius r about the centre O. The particle moves from A to B through the circumference of the circle.

The angular displacement of the particle is for time t. Then angular speed is .

If the distance travelled by the particle is arc AB = then = .

So, = = [where linear speed v = ]

v = .

Angular acceleration: The change of angular velocity per unit time is called angular acceleration.

If is the change of angular velocity for time then angular acceleration is .

SI unit of angular acceleration is .

Dimension of angular acceleration is .

Relation between linear acceleration and angular acceleration: A particle rotates in a circular path of radius r about the centre O. The particle moves from A to B through the circumference of the circle for time .

The change of angular velocity of the particle from A to B is . Then angular acceleration is .

If is the change in linear velocity of the particle from A to B then linear acceleration [as v = r so, = r where r is constant].

So, a = r.

Video explanation of this post.

Relations between angular displacement, angular velocity and angular acceleration:

(i) Let us consider a particle is rotating with uniform angular velocity . Then it accelerates uniformly with and after time t its final angular velocity .

Then = +t .

(ii)Let us consider a particle is rotating with uniform angular velocity . Then it accelerates uniformly with and after time t its angular displacement is .

Then = t + .

(iii)Let us consider a particle is rotating with uniform angular velocity .Then it accelerates uniformly with and afterangular displacement , its final angular velocity . Then = + 2 .